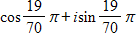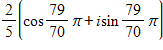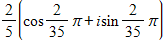Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.12 + 42 + 72 + . . . + (3n - 2)2 = 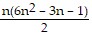
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 1 = 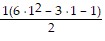 = 1.
= 1.
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
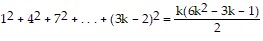 is true for some positive integer k.
is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
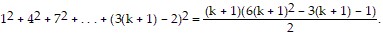
So we assume that 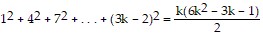 is true and add the next term,
is true and add the next term, 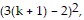 to both sides of the equation.
to both sides of the equation.
12 + 42 + 72 + . . . + (3k - 2)2 + (3(k + 1) - 2)2 =  + (3(k + 1) - 2)2
+ (3(k + 1) - 2)2
= 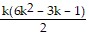 + (3k + 1)2
+ (3k + 1)2
= 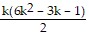 +
+ 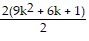
= 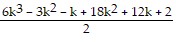
= 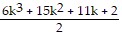
Simplify the expression 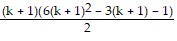 to verify:
to verify:
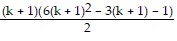 =
= 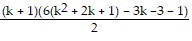
= 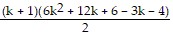
= 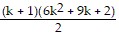
= 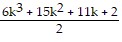
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Combine like terms, if possible.4t + 4 - 4t
A. 4 B. 8t C. 8t + 4 D. -8t + 4
Find the midpoint of the line segment joining the points P1 and P2.P1 = (7, 1); P2 = (-16, -16)
A. 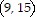
B. 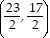
C. 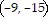
D. 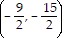
Solve the problem.Find all values of k so that the given points are  units apart. (-5, 5), (k, 0)
units apart. (-5, 5), (k, 0)
A. 7 B. 3, 7 C. -3, -7 D. -7
Divide the complex numbers below and leave the result in trigonometric form.

A. 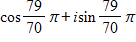
B. ?
C. ?
D. ?
E. ?