Consider the following benefit and cost functions: B(X) = 600X-12X² and C(X) = 20X²
a) What are the MB and the MC?
b) What level of X maximizes the net benefit?
c) What is the net benefit (NB)?
a) Marginal benefit function (MB) = derivating of total benefit function = 600 - 24X.
Marginal cost function (MC) = derivating of total cost function = 40X.
b) Net benefit = Total benefit - Total cost = 600X -12X2 - 20X2 = 600 - 32X2
Now the level of X that maximizes the net benefit equates MB and MC
600 - 24X = 40X
X = 600/64 = 9.375
C) Net benefit (NB) = 600 - 32*(9.375)^2 = -2212.5
You might also like to view...
The figure below shows a firm that has two plants. Plant 1 has a marginal cost curve of mc1, plant 2 has a marginal cost curve of mc2, and the overall marginal cost curve is MC. When the managers maximize profit, the marginal cost in plant 1 is ________ and the marginal cost in plant 2 is ________ .
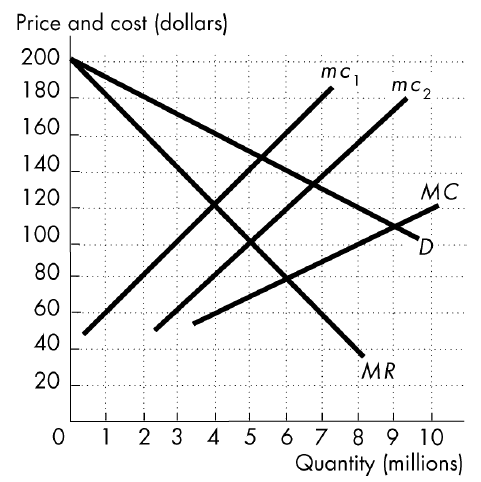
A) $160; $150
B) $80 per unit; $80 per unit
C) $120; $100
D) None of the above answers is correct.
Labor markets are generally perfectly competitive markets
a. True b. False Indicate whether the statement is true or false
Suppose net domestic product is $4.8 billion, net income earned abroad is $0.7 billion, other business income adjustments net of indirect business taxes and transfers are $0.4 billion, and personal income taxes are $0.8 billion. Then, national income equals
A. $6.7 billion. B. $5.9 billion. C. $2.9 billion. D. $3.6 billion.
In the long run, perfectly competitive firms earn zero economic profit. Why do firms enter an industry when they know that in the long-run they will not earn any profit?
What will be an ideal response?