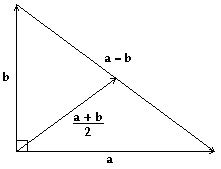
Solve the problem.Show that the midpoint of the hypotenuse of a right triangle is equidistant from all three vertices. [Hint: See the figure below. Show that 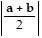 =
= 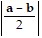 .]
.] 
What will be an ideal response?
Verify that 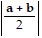 =
= 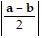 .
.
Cancel the 2's and square both sides: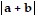 2 =
2 = 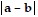 2 or
2 or
(a + b)?(a + b) = (a - b)?(a - b) or
a?a + 2a?b + b?b = a?a - 2a?b + b?b [2a?b = 0 since a and b are orthogonal]
a?a + b?b = a?a + b?b Verified.
Thus, the midpoint is equidistant from all three vertices.
You might also like to view...
Use Stokes' Theorem to calculate the circulation of the field F around the curve C in the indicated direction.F = -3yi - 5xj - 2z3k ; C: the portion of the plane 8x + 8y + 3z = 8 in the first quadrant
A. -2 B. - 1 C. 1 D. 0
Find the requested angle.What is the measure of an angle whose measure is nine times its supplement?
A. 159° B. 165° C. 180° D. 162°
Perform the operation. Write the answer as a fraction in lowest terms.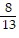 -
- 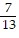
A. 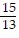
B. 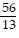
C. 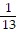
D. 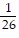
Determine whether the pair of lines is parallel, perpendicular, or neither. 9x + 3y = 1218x + 6y = 27
A. parallel B. perpendicular C. neither