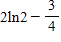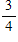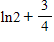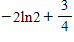The result of a hypothesis is described in terms of the probability of obtaining a particular sample. Use the given context to formulate the null and alternative hypotheses. Discuss whether the sample provides evidence for rejecting the null hypothesis.A company claims that it pays women the same as men for comparable work. The union decides to investigate this claim. The mean monthly salary for men in entry level positions is $2250. Amongst a random sample of 60 female employees in similar positions , the mean monthly salary was $2210. Assuming that the mean salary for all female employees in entry level positions is $2250, the probability of selecting a sample in which the mean monthly salary is $2210 or less is 0.06.
What will be an ideal response?
Null hypothesis: mean monthly salary for female entry level employees = $2250
Alternative hypothesis: mean monthly salary for female entry level employees < $2250
The result is not significant at the 0.05 level, there is insufficient evidence to conclude that the company pays female entry level employees less than male entry level employees.
You might also like to view...
Express as a product of prime factors.2600
A. 23 ? 52 ? 13 B. 2 ? 54 ? 13 C. 23 ? 53 ? 13 D. 24 ? 5 ? 13
Sketch the graph of f(x). Determine the domain, range, and the equation of the horizontal asymptote of the function.f(x) = ex - 5
A. Domain: (-?, ?), range: (-5, ?)
Horizontal asymptote: y = -5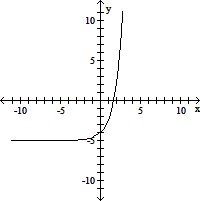
B. Domain: (-?, ?), range: (5, ?)
Horizontal asymptote: y = 5
C. Domain: (-?, ?), range: (-?, 5)
Horizontal asymptote: y = 5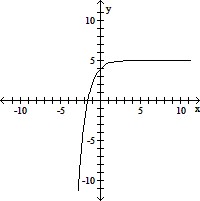
D. Domain: (-?, ?), range: (-5, ?)
Horizontal asymptote: y = -5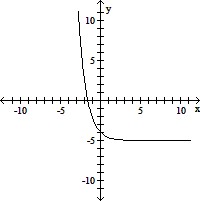
Determine whether f and g are inverses by determining whether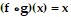 
and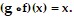 
f(x) = 
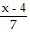, g(x) = -7x + 4
A. Yes B. No
Evaluate the definite integral by using the method of integration by parts.
?
?
A. ?
B. ?
C. ?
D. ?
E. ?