Use a Riemann sum to approximate the area under the graph of f(x) on the given interval. Use the left endpoints.f(x) = 4x3; 0 ? x ? 3, n = 6
A.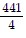 
= 110.25
B.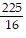 
= 14.06
C.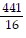 
= 27.56
D.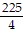 
= 56.25
Answer: D
You might also like to view...
Write the equation for the plane.The plane passing through the point P0(-3, 1, 7) that is perpendicular to the line x = -1 + 6t, y = 2 - 5t,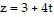 
A. 4x + 9y + 2z = 11 B. -3x + y + 7z = 68 C. 6x - 5y + 4z = 5 D. -x + 2y + 3z = 26
Find y '.y =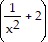 
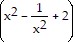
A.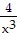 
+ 4x
B. 
+ 4x
C. - 
+ 4x
D. - 
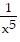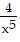- 4x
Construct a truth table for the statement.(~p ? q) ? (p ? q)
A.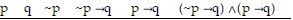 
T T F F F F
T F F F T F
F T T F F F
F F T T F F
B.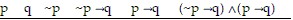 
T T F T T T
T F F T F F
F T T T T T
F F T F T T
C.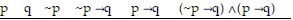 
T T F T T T
T F F T F F
F T T T T T
F F T F T F
D.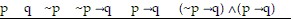 
T T F F F F
T F F F T T
F T T F F F
F F T T F T
A delivery truck must deliver packages to 6 different store locations (A, B, C, D, E, and F). The trip must start and end at A. The graph below shows the distances (in miles) between locations. We want to minimize the total distance traveled.
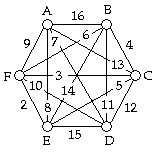Using only the nearest-neighbor, repetitive nearest-neighbor, and cheapest-link algorithms (not brute force) on this graph,
A. the cheapest-link and the repetitive nearest-neighbor algorithms both yield the shortest trip. B. the nearest-neighbor algorithm yields the shortest trip. C. the nearest-neighbor and the repetitive nearest-neighbor algorithms both yield the shortest trip. D. the repetitive nearest-neighbor algorithm yields the shortest trip. E. the cheapest-link algorithm yields the shortest trip.