Graph the quadratic function. Determine the vertex, find the equation of the axis of symmetry, find any x- and y-intercepts, and state the domain and range in interval notation.f(x) = -11x2 - 2x - 12
A. vertex: 
axis of symmetry: x = 
x-intercept: none; y-intercept: 12
domain: (-?, ?); range: 
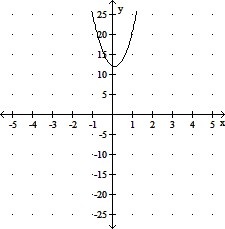
B. vertex: 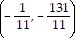
axis of symmetry: x = - 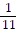
x-intercept: none; y-intercept: -12
domain: (-?, ?); range: 

C. vertex: 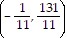
axis of symmetry: x = - 
x-intercept: none; y-intercept: 12
domain: (-?, ?); range: 

D. vertex: 
axis of symmetry: x = 
x-intercept: none; y-intercept: -12
domain: (-?, ?); range: 

Answer: B
You might also like to view...
Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola.x2 - 25y2 - 8x - 100y - 109 = 0
A. center at (4, -2)
transverse axis is parallel to x-axis
vertices at (-1, -2) and (9, -2)
foci at (4 - 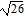 , -2) and (4 +
, -2) and (4 + 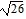 , -2)
, -2)
asymptotes of y + 2 = - 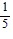 (x - 4) and y + 2 =
(x - 4) and y + 2 = 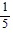 (x - 4)
(x - 4)
B. center at (4, -2)
transverse axis is parallel to x-axis
vertices at (3, -2) and (5, -2)
foci at (4 - 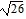 , -2) and (4 +
, -2) and (4 + 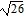 , -2)
, -2)
asymptotes of y + 2 = - 5(x - 4) and y + 2 = 5(x - 4)
C. center at (-2, 4)
transverse axis is parallel to x-axis
vertices at (-7, 4) and (3, 4)
foci at (-2 - 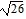 , 4) and (-2 +
, 4) and (-2 + 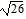 , 4)
, 4)
asymptotes of y - 4 = - 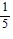 (x + 2) and y - 4 =
(x + 2) and y - 4 = 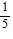 (x + 2)
(x + 2)
D. center at (4, -2)
transverse axis is parallel to y-axis
vertices at (4, -7) and (4, 3)
foci at (4, -2 - 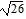 ) and (4, -2 +
) and (4, -2 +  )
)
asymptotes of y - 2 = - 5(x + 4) and y - 2 = 5(x + 4)
Decide whether or not the functions are inverses of each other.f(x) = 6x - 5, g(x) = 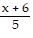
A. Inverses B. Not inverses
Perform the indicated operations and simplify the result. Leave the answer in factored form.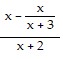
A. 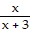
B. 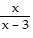
C. 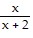
D. 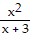
Solve the equation by completing the square.7x2 + 20x = -14
A. 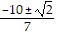
B. 
C. 
D. 