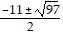Divide. Round the quotient as indicated.6.61 ÷ 0.086; hundredths place
A. 77.36
B. 7.74
C. 76.86
D. 7.69
Answer: C
You might also like to view...
Solve the problem.Find the area under y =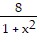 
in the first quadrant.
A. 8? B. 4? C. 2? D. 16?
Perform the specified translation.The graph on the left is the graph of the function defined by y = f(x).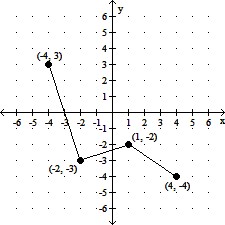 
Sketch a graph of the function defined by the equation y = f(x) + 2. Describe the type of shift that was performed on the original graph.
A. A vertical shift of the graph of y = f(x),
2 units upward.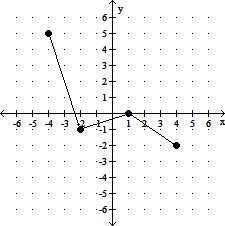
B. A horizontal shift of the graph of y = f(x),
2 units to the left.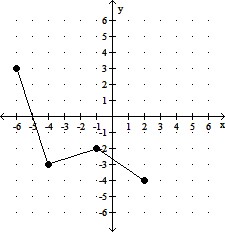
C. A horizontal shift of the graph of y = f(x),
2 units to the right.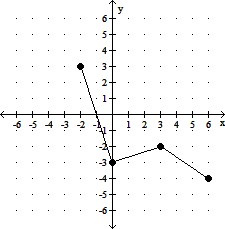
D. A vertical shift of the graph of y = f(x),
2 units downward.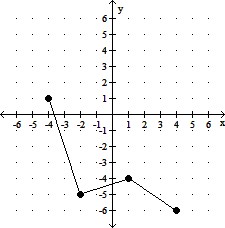
Solve the problem. Suppose a student plans to drive from his home to New Haven 75 miles on a divided highway and 30 miles on an undivided highway. The speed limit is 70 mph on the divided highway and 50 mph on the undivided highway. Assume the driver drives nonstop. Let T(a) represent the driving time (in hours) if the student drives at a mph above the speed limits. By finding a formula for T(a), determine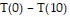 
. What does your result mean in terms of the trip?
A. T(0) - T(10) = 0.23; the trip will take 0.23 hours more by driving at 10 mph over the speed limits than it would take driving at the speed limits. B. T(0) - T(10) = 0.37; the trip will take 0.37 hours less by driving at 10 mph over the speed limits than it would take driving at the speed limits. C. T(0) - T(10) = 0.37; the trip will take 0.37 hours more by driving at 10 mph over the speed limits than it would take driving at the speed limits. D. T(0) - T(10) = 0.23; the trip will take 0.23 hours less by driving at 10 mph over the speed limits than it would take driving at the speed limits.
Find the zeros of the function. Give exact answers.f(x) = 2x2 + 11x + 3
A.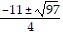 
B.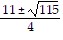 
C.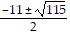 
D. 