Write the statement as an absolute value inequality.x is within 3 units of 2
A. |3 - x| < 2
B. |x - 2| ? 3
C. |x - 2| < 3
D. |x - 3| < 2
Answer: B
You might also like to view...
Convert to logarithmic form.41/2 = 2
A. log 2 4 = 1/2 B. log 2 1/2 = 4 C. log 1/2 4 = 2 D. log 4 2 = 1/2
Solve the equation by factoring.12x2 - 5x - 25 = 0
A. 
B.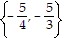 
C. 
D.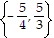 
Solve the problem.The amount of paint needed to cover the walls of a room varies jointly as the perimeter of the room and the height of the wall. If a room with a perimeter of 50 feet and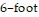 
walls requires 
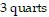of paint, find the amount of paint needed to cover the walls of a room with a perimeter of 60 feet and 6-foot walls.
A. 3.6 qt B. 360 qt C. 7.2 qt D. 36 qt
Solve the problem.A company that produces handbags has found that revenue from the sales of the handbags is $10 per handbag, less sales costs of $100. Production costs are $125, plus $9 per handbag. Profit (P) is given by revenue (R) less cost (C), so the company must find the production level x that makes P > 0, that is, R - C > 0.(a) Write an expression for revenue, R, letting x represent the production level (number of handbags to be produced.)(b) Write an expression for production costs C in terms of x.(c) Write an expression for profit P, and then solve the inequality P > 0.(d) Describe the solution in terms of the problem.
A. (a) R = 10x - 100; (b) C = 75 + 11x; (c) P = (10x - 100) - (75 + 11x) = x - 125; x > 125; (d) To make a profit, more than 125 handbags must be produced and sold. B. (a) R = 10x + 100; (b) C = 125 + 9x; (c) P = (10x + 100) - (125 + 9x) = x - 25; x > 25; (d) To make a profit, more than 25 handbags must be produced and sold. C. (a) R = 10x - 100; (b) C = 125 - 9x; (c) P = (10x - 100) - (125 - 9x) = x - 175; x > 175; (d) To make a profit, more than 175 handbags must be produced and sold. D. (a) R = 10x - 100; (b) C = 125 + 9x; (c) P = (10x - 100) - (125 + 9x) = x - 225; x > 225; (d) To make a profit, more than 225 handbags must be produced and sold.