Use mathematical induction to prove that the statement is true for every positive integer n.n! > 3n, for n ? 4
What will be an ideal response?
Answers will vary. One possible proof follows.
a). 4! > 3?4, so the statement is true for n = 4.
b). Assume the statement is true for n = k ? 4. Then,
k! > 3k, or
(k)(k-1). . .(1) > 3k.
Multiply both sides by (k + 1):
(k + 1)(k)(k-1). . .(1) = (k + 1)! > 3(k+1)k
Since k > 1, then (k + 1)k > (k + 1), so we can write
(k + 1)! > 3(k + 1)k > 3(k + 1), or
(k + 1)! > 3(k + 1)
The statement is true for n = k + 1 if it is true for n = k, and it is true for n = 4. Therefore, the statement is true for all n ? 4.
You might also like to view...
A dosage of 15 mg of a medication has been ordered. The medication label reads 7.5 mg per tablet. How many tablets should be given to the patient?
A. 1.5 tablets B. 3 tablets C. 2 tablets D. 0.5 tablets
Simplify the radical.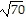
A. Cannot be simplified
B. 2
C. 4
D. 35
Solve the problem.A bridge is built in the shape of a semielliptical arch. It has a span of 118 feet. The height of the arch 26 feet from the center is to be 5 feet. Find the height of the arch at its center.
A. 11.35 ft B. 5.13 ft C. 5.57 ft D. 26.09 ft
Analyze the graph of the given function f as follows:(a) Determine the end behavior: find the power function that the graph of f resembles for large values of |x|.(b) Find the x- and y-intercepts of the graph.(c) Determine whether the graph crosses or touches the x-axis at each x-intercept.(d) Graph f using a graphing utility.(e) Use the graph to determine the local maxima and local minima, if any exist. Round turning points to two decimal places.(f) Use the information obtained in (a) - (e) to draw a complete graph of f by hand. Label all intercepts and turning points.(g) Find the domain of f. Use the graph to find the range of f.(h) Use the graph to determine where f is increasing and where f is decreasing.f(x) = 16x - x3
What will be an ideal response?