Solve the problem.What conditions, when present, are sufficient to conclude that a function f(x) has a limit as x approaches some value of a?
A. The limit of 
as 
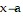from the left exists, the limit of 
as 
from the right exists, and these two limits are the same.
B. The limit of 
as 
from the left exists, the limit of 
as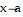 
from the right exists, and at least one of these limits is the same as f(a).
C. f(a) exists, the limit of 
as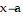 
from the left exists, and the limit of 
as 
from the right exists.
D. Either the limit of 
as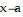 
from the left exists or the limit of 
as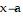 
from the right exists
Answer: A
You might also like to view...
Calculate the derivative of the function. Then find the value of the derivative as specified.f(x) = x2 + 7x - 2; f '(0)
A. f '(x) = 2x; f '(0) = 0 B. f '(x) = 2x + 7; f '(0) = 7 C. f '(x) = x + 7; f '(0) = 7 D. f '(x) = 2x - 2; f '(0) = - 2
Identify the form of the argument and state whether the argument is valid or invalid.If you eat well, you will be well.If you are well, you will be happy.Therefore, if you eat well, you will be happy.
A. Fallacy of the inverse; invalid B. Law of contraposition; valid C. Law of syllogism; valid D. Fallacy of the converse; invalid
Solve the problem.Sketch a graph that depicts the amount of water in a 50-gallon tank. The tank is initially full, And then a pump is used to take water out of the tank at a rate of 4 gallons per minute. This pump is turned off after 6 minutes and at that same time a different pump is turned on. This second pump puts water into the tank at a rate of 2 gallons per minute for 4 minutes.
A. 
B.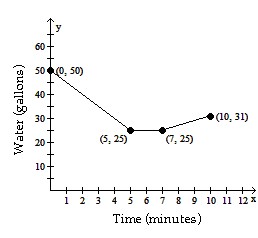 
C. 
D. 
Determine whether the pair of lines is parallel, perpendicular, or neither.y = -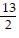 
x + 4y = 
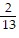x + 4
A. Parallel B. Perpendicular C. Neither