Solve the problem.A simple model of a harvested resource follows the equation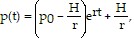 
where p(t) is the amount (or population) of the resource at time 
is the natural growth rate of the resource, and 
is the harvesting rate. If 
/> and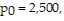 
for what values of H is the amount of the resource increasing? For what value of H is the amount of the resource constant?
A. H < 125; H > 125
B. H < 125; H = 125
C. H < 50; H < 50
D. H > 125; H = 125
Answer: B
You might also like to view...
Solve the problem.Suppose that the average monthly low temperatures for a small town are shown in the table.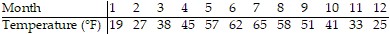
Find a function of the form y = A sin B(x - C) + D that models this data.
A. f(x) = 23 sin 
+ 42
B. f(x) = 42 sin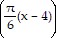 
+ 23
C. f(x) = 23 sin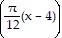 
+ 42
D. f(x) = 23 sin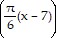 
+ 42
Write the algebraic expression described. Simplify if possible.During a walk-a-thon, Rosilyn walked 14 fewer laps than June walked. If June walked b laps, how many laps did Rosilyn walk?
A. (b - 14) laps
B. (14 - b) laps
C.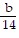 
laps
D. (b + 14) laps
Simplify the expression.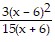
? 
A.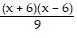 
B.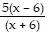 
C.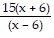 
D. 
Solve the problem.Ken is 6 feet tall and is walking away from a streetlight. The streetlight has its light bulb 14 feet above the ground, and Ken is walking at the rate of 1.7 feet per second. Find a function, d(t), which gives the distance Ken is from the streetlight in terms of time. Find a function,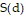 
, which gives the length of Ken's shadow in terms of d. Then find 
.
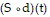A. (S ? d)(t) = 1.62t B. (S ? d)(t) = 0.94t C. (S ? d)(t) = 2.87t D. (S ? d)(t) = 1.28t