Solve the equation.3(2z - 3) = 5(z + 4)
A. 11
B. 29
C. 14
D. -11
Answer: B
You might also like to view...
Solve the problem.Use a graphical method to determine the approximate interval for which the second order Taylor polynomial for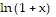 
at 
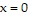approximates 
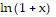with an absolute error of no more than 0.04.
A. -0.4310 ? x ? 0.5525 B. -0.5525 ? x ? 0.5525 C. -0.1928 ? x ? 0.7063 D. -0.5525 ? x ? 0.2640
Solve.The seats in the lecture hall are arranged in 16 rows with 9 seats in each row. Find how many seats are in this room.
A. 144 seats B. 153 seats C. 135 seats D. 154 seats
Perform the indicated operations. Write the answer using only positive exponents. Assume all variables represent positive real numbers.(9k2m-4)1/2
A.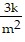 
B. 3km2
C. 2km2
D.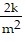 
Postal regulations specify that the combined length and girth of a parcel sent by parcel post may not exceed 120 in. Find the dimensions of the rectangular package that would have the greatest possible volume under these regulations. (Hint: Let the dimensions of the box be x'' by y'' by z'' (see the figure below). Then,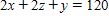 
, and the volume
src="https://sciemce.com/media/3/ppg__cognero__8.3_Maxima_and_Minima_of_Functions_of_Several_Variables__media__83349d6a-c74d-453f-ab65-4862ad47be6b.PNG" style="vertical-align:middle;" />. So that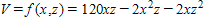 
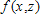
. Maximize 
.)
?
?
A. x = 20 inches, y = 40 inches, z = 20 inches, V = 16,000 cubic inches
B. x = 20 inches, y = 20 inches, z = 17 inches, V = 6,800 cubic inches
C. x = 22 inches, y = 40 inches, z = 22 inches, V = 16,000 cubic inches
D. x = 22 inches, y = 39 inches, z = 17 inches, V = 14,586 cubic inches
E. x = 22 inches, y = 40 inches, z = 17 inches, V = 14,586 cubic inches