How would you find the area of a circle, given the area of the sector with radius 30 feet, and central angle 120??
??
A.
120? is 1/4 of a circle's revolution; Therefore, the area of the circle is 4 times the area of the sector.
B.
?120? is 1/3 of a circle's revolution; Therefore, the area of the circle is 3 times the area of the sector.
C.
?120? is 1/4 of 180?; Therefore, the area of the circle is 4 times the area of the sector.
D.
?The area of the circle is: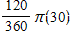 
.
E.
?b and d are correct.
Answer: B
You might also like to view...
Use the trapezoidal rule to find the area.A pool was measured every 1.50 yd. The distances across the pool (in yards) are given in the diagram. Find the area.
A. 33.2 yd2 B. 35.5 yd2 C. 50.4 yd2 D. 53.8 yd2
The Richter scale converts seismographic readings into numbers for measuring the magnitude of an earthquake according to this function M(x) = log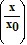 
, where x0 = 10-3.Find the magnitude (to one decimal place) of an earthquake whose seismographic reading is 2000 millimeters at a distance of 100 kilometers from its epicenter. Round the answer to the nearest tenth.
A. 5.9 B. 7.3 C. 6.3 D. 6.4
Convert the angle in radians to degrees.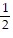
?
A. 180° B. 144° C. 90° D. 360?°
Find the length of the brace needed in the illustration. Use the rules for working with measurements.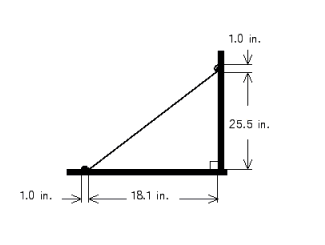
A. b = 33.3 in. B. b = 35.5 in. C. b = 30 in. D. b = 34.4 in. E. b = 45.6 in.