Determine whether the matrix is an absorbing stochastic matrix. Give a reason for your conclusion.
What will be an ideal response?
No; there is no absorbing state.
Mathematics
You might also like to view...
Find the standard-form equation of the hyperbola centered at the origin which satisfies the given conditions.Vertices at (3, 0) and (-3, 0); foci at (8, 0) and (-8, 0)
A.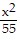 
- 
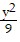= 1
B. 
- 
= 1
C. 
- 
= 1
D. 
- 
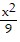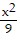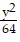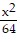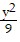= 1
Mathematics
State the degree and leading coefficient of the polynomial function.f(x) = -13x4 - 6x3 - 7x2 + 9
A. Degree: 10; leading coefficient: -13 B. Degree: 4; leading coefficient: -13 C. Degree: 3; leading coefficient: -13 D. Degree: -13; leading coefficient: -7
Mathematics
Use the simplex method to solve.Minimize 3x + 2y subject to the following constraints.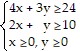
What will be an ideal response?
Mathematics
Solve the equation.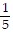
(r + 6) = 
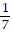(r + 8)
A. 1 B. 2 C. -2 D. -1
Mathematics