Answer each question appropriately.If differentiable functions y = F(x) and y = G(x) both solve the initial value problem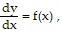 
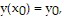on an interval I, must 
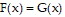for every x in I? Justify the answer.
A. F(x) = G(x) for every x in I because integrating f(x) results in one unique function.
B. F(x) = G(x) for every x in I because when given an initial condition, we can find the integration constant when integrating f(x). Therefore, the particular solution to the initial value problem is unique.
C. There is not enough information given to determine if F(x) = G(x).
D. F(x) and G(x) are not unique. There are infinitely many functions that solve the initial value problem. When solving the problem there is an integration constant C that can be any value. F(x) and G(x) could each have a different constant term.
Answer: B
You might also like to view...
Find the limit and determine if the function is continuous at the point being approached.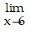
sin (x sin2 (x) + x cos2 (x) + 2)
A. sin 8; yes B. sin -4; yes C. sin 8; no D. Does not exist; no
For the given function, find the domain and range of both f(x) and f-1(x).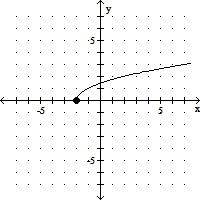
A.
| f: | domain: {x| x ? -2} |
f-1: domain: {x| x ? 0}
range: {y| y ? -2}
B.
| f: | domain: {x| x ? -2} |
f-1: domain: {x| x ? -2}
range: {y| y ? 0}
C.
| f: | domain: {x| x ? 0} |
f-1: domain: {x| x ? -2}
range: {y| y ? 0}
D.
| f: | domain: {x| x ? 0} |
f-1: domain: {x| x ? 0}
range: {y| y ? -2}
Find the x-intercept(s) and the y-intercept of the function.g(x) = 8x + 3
A.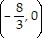 
, (0, 3)
B. 
, (-3, 0)
C. 
, (0, 3)
D. 
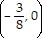, (0, 3)
Solve the problem.Edwin has a board that is 20 feet long. He wants to cut the board into pieces that are 2.5 feet long. How many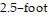 
pieces will he get from the large board?
A. 9 pieces B. 7 pieces C. 8 pieces D. 80 pieces