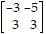Solve the problem.Find the center of mass of the region of constant density bounded by the paraboloid 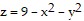 and the xy-plane.
and the xy-plane.
A. 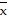 = 0,
= 0, 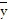 = 0,
= 0,  = 1
= 1
B. 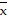 = 0,
= 0, 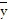 = 0,
= 0,  =
= 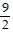
C. 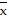 = 0,
= 0, 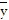 = 0,
= 0,  =
= 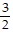
D. 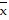 = 0,
= 0, 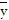 = 0,
= 0,  = 3
= 3
Answer: D
You might also like to view...
Find the area of the rectangle or square.
 14 ft
14 ft
A. 49 square feet B. 196 square feet C. 98 square feet D. 147 square feet
Solve.81x2 + 4y2 = 3242y - 9x = 18
A. (0, -9), (2, 0) B. (0, 9), (-2,0) C. (0, -2), (9, 0) D. (0, 2), (0, -9)
Solve the problem.Find an equation of the form 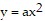 that describes the outline of a satellite dish such that the bottom of the dish passes through (0, 0), the diameter of the dish is 24 inches, and the depth of the dish is 5 inches
that describes the outline of a satellite dish such that the bottom of the dish passes through (0, 0), the diameter of the dish is 24 inches, and the depth of the dish is 5 inches
A. y =  x2
x2
B. y = 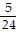 x2
x2
C. y = 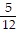 x2
x2
D. y = 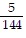 x2
x2
Encode or decode the given message, as requested, numbering the letters of the alphabet 1 through 26 in their usual order.Use the coding matrix A =  to encode the message LIFE.
to encode the message LIFE.
A. 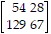
B. 
C. 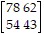
D.