State the dual problem. Use y1, y2, y3 and y4 as the variables. Given: y1 ? 0, y2 ? 0, y3 ? 0, and y4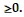 Maximizez = 3x1 + 2x2subject to:x1 + x2 ? 14 2x1 + x2 ? 28 x1 ? 0, x2 ? 0
Maximizez = 3x1 + 2x2subject to:x1 + x2 ? 14 2x1 + x2 ? 28 x1 ? 0, x2 ? 0
A.
| Minimize | w = 28y1 + 14y2 |
| subject to: | 2y1 + y2 ? 3 |
B.
| Minimize | w = 14y1 + 28y2 |
| subject to: | y1 + 2y2 ? 3 |
C.
| Minimize | w = 28y1 + 14y2 |
| subject to: | 2y1+ y2 ? 3 |
D.
| Minimize | w = 14y1 + 28y2 |
| subject to: | y1 + 2y2 ? 3 |
Answer: D
You might also like to view...
Find an equation of a parabola satisfying the given conditions.Find the equation of the parabola with vertex at the origin and axis along the x-axis if the parabola passes through the point 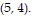
A. x2 =  y
y
B. y2 = 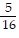 x
x
C. x2 = 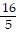 y
y
D. y2 = 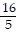 x
x
Provide an appropriate response.Use logarithmic differentiation to find 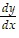 from y =
from y = 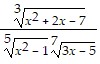 .
.
What will be an ideal response?
Multiply the polynomials using the special product formulas. Express the answer as a single polynomial in standard form.(x + 4y)(x - 4y)
A. x2 - 8xy - 16y2 B. x2 - 16y2 C. x2 + 8xy - 16y2 D. x2 - 8y2
Use the Leading Coefficient Test to determine the end behavior of the polynomial function.f(x) = x3(x - 4)(x + 2)2
A. y ? -? as x ? -? and y ? -? as x ? ? B. y ? ? as x ? -? and y ? ? as x ? ? C. y ? ? as x ? -? and y ? -? as x ? ? D. y ? -? as x ? -? and y ? ? as x ? ?