Select the graph of the equation as a circle, a parabola, an ellipse, or a hyperbola.
?
?
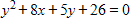
A. Ellipse
B. Hyperbola
C. Circle
D. Parabola
E. None of the above
Answer: D
You might also like to view...
Find the center of mass of a thin plate of constant density covering the given region.The region bounded by y = x4, x = 3, and the x-axis
A.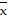 
= 
, 
= 
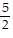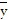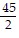
B. 
= 
, 
= 
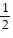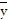C. 
= 
, 
= 
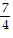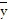D. 
= 
, 
= 
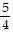Find the exact value of the trigonometric function. Do not use a calculator or tables.cos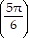 
A. 
B. - 
C. - 
D. - 
Find f(x) and g(x) such that h(x) = (f ? g)(x).h(x) = 
A. f(x) = 
, g(x) = 
B. f(x) = 
, g(x) = 
C. f(x) = 
, g(x) = 
D. f(x) =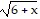 
, g(x) =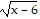 
Suppose that John hands you a coin to flip and wants to bet on the outcome. Now, John has tried this sort of thing before, and you suspect that the coin is "rigged." You decide to test this hypothesis by taking a sample. You flip the coin twice, and it is heads both times. You say, "Aha, I knew it was rigged!" John replies, "Don't be silly. Any coin can come up heads twice in a row."
? The following scheme was devised by mathematician John von Neumann to allow fair results even if the coin is somewhat biased. The coin is flipped twice. If it comes up heads both times or tails both times, it is flipped twice again. If it comes up heads-tails, this will decide the outcome in favor of the first party; and if it comes up tails-heads, this will decide the outcome in favor of the second party. Show that this will result in a fair toss even if the coins are biased. What will be an ideal response?