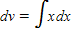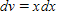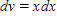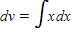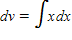Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.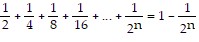
What will be an ideal response?
When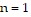 
, the left side of the statement is 
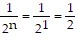, and the right side of the
statement is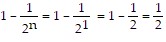 
, so the statement is true when 
.
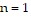Assume the statement is true for some natural number k. Then,
.
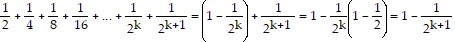So the statement is true for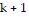 
. Conditions I and II are satisfied; by the Principle of Mathematical Induction, the statement is true for all natural numbers.
Mathematics
You might also like to view...
Identify u and dv for finding the integral using integration by parts.
?
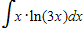
A.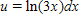 
; 
B.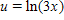 
;
C.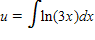 
;
D.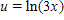 
;
E.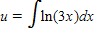 
;
Mathematics
Use a table and/or graph to find the asymptotes of the function.f(x) =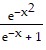 
A. x = 0, y = 0 B. x = 0 C. y = 0 D. No asymptotes
Mathematics
Find the additive inverse of the number.21
A. 0
B. 21
C.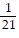 
D. -21
Mathematics
Find the absolute value.|-4|
A. 4 B. 0 C. -4 D. 8
Mathematics