Use mathematical induction to prove the following.If a is a constant and 0 < a < 1, then an < 1.
What will be an ideal response?
Answers may vary. One possibility:
Sn: If a is a constant and 0 < a < 1, then an < 1.
S1: If a is a constant and 0 < a < 1, then a1 < 1.
Sk: If a is a constant and 0 < a < 1, then ak < 1.
Sk+1: If a is a constant and 0 < a < 1, then ak+1 < 1.
1. Basis step: Since it is given that a < 1, then a1 < 1. Therefore, S1 is true.
2. Induction step: Let k be any natural number. Assume Sk. Deduce Sk+1.
If a is a constant and 0 < a < 1, then ak < 1.
If a is a constant and 0 < a < 1, then ak ? a < 1 ? a. Multiplying by a, a > 0
If a is a constant and 0 < a < 1, then ak+1 < a.
If a is a constant and 0 < a < 1, then ak+1 < a < 1. Given a < 1
If a is a constant and 0 < a < 1, then ak+1 < 1.
You might also like to view...
Set up the iterated integral for evaluating 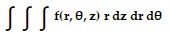 over the given region D. DD is the right circular cylinder whose base is the circle
over the given region D. DD is the right circular cylinder whose base is the circle 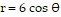 in the xy-plane and whose top lies in the plane
in the xy-plane and whose top lies in the plane 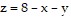 .
.
A. 
B. 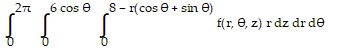
C. 
D. 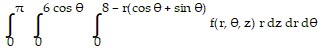
Find the rectangular equation of the given polar equation.r = 
A. y2 + 10x - 25 = 0 B. x2 - 10y + 25 = 0 C. x2 + 10y - 25 = 0 D. y2 - 10x + 25 = 0
Find the compound interest earned. Round to the nearest cent. Use your calculator, rather than the tables.$8000 at 8% compounded annually for 4 years
A. $2077.70 B. $2560.00 C. $641.50 D. $2883.91
Multiply.(y + 7)(y - 1)
A. y2 + 6y - 7 B. 2y - 7 C. y2 - 6y + 7 D. 2y2 + 7