Solve the problem.Rachel's bus leaves at 7:25 PM and accelerates at the rate of 3 meters per second per second. Rachel, who can run 8 meters per second, arrives at the bus station 3 seconds after the bus has left. Find parametric equations that describe the motions of the bus and Rachel as a function of time. Determine algebraically whether Rachel will catch the bus. If so, when?
A. Bus: x1 = 
t2, y1 = 2; Rachel: x2 = 8(t - 3), y2 = 4
Rachel will catch the bus at 7:30 PM
B. Bus: x1 = 
t2, y1 = 2; Rachel: x2 = 8(t - 3), y2 = 4
Rachel won't catch the bus.
C. Bus: x1 = 3t2, y1 = 2; Rachel: x2 = 4(t - 3), y2 = 4
Rachel will catch the bus at 7:29 PM
D. Bus: x1 = 
t2, y1 = 2; Rachel: x2 = 8(t + 3), y2 = 4
Rachel won't catch the bus.
Answer: B
You might also like to view...
Find the sum of the series by recognizing how it is related to something familiar.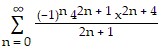
A. e3x tan-1 4x
B.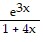 
C. x3 tan-1 4x
D. x-3 tan-1 4x
Find the prime factorization of the composite number.177
A. 32 B. 3 × 57 C. 32 × 59 D. 3 × 59
Provide an appropriate response.Change 500 inches to meters. (Round to nearest tenth; 1 m = 39.37 in.)
A. 12.8 B. 196.85 C. 19,685 D. 12.7 E. none of the above
Determine the row operation that was used on the first matrix to obtain the second matrix.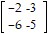
, 
What will be an ideal response?