Solve the problem. Assume that relative maximum and minimum values are absolute maximum and minimum values.A firm produces two kinds of tennis balls, one for recreational players which sells for $2.50 per can, and one for serious players which sells for $4.00 per can. The total revenue from the sale of x thousand cans of the first ball and y thousand cans of the second ball is given by 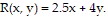The company determines that the total cost, in thousands of dollars, of producing x thousand cans of the first ball and y thousand cans of the second ball is given by 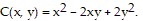Find the

Question

number of each type of ball which must be produced and sold in order to maximize the profit.

A. 2000 of the $2.50 cans and 5000 of the $4.00 cans
B. 4000 of the $2.50 cans and 3000 of the $4.00 cans
C. 3000 of the $2.50 cans and 4000 of the $4.00 cans
D. 5000 of the $2.50 cans and 3000 of the $4.00 cans

Answer 1

Answer: B