Solve the problem.A music group out of Bakersfield, California is planning to appear in the following cities: Los Angeles, California; San Diego, California; Fresno, California; and Las Vegas, Nevada. The distances between these locations in miles are listed below: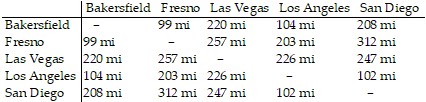
Use the nearest-neighbor algorithm to find a Hamilton circuit beginning at Bakersfield.
A. Bakersfield ? San Diego ? Los Angeles ? Fresno ? Las Vegas ? Bakersfield
B. Bakersfield ? Los Angeles ? San Diego ? Las Vegas ? Fresno ? Bakersfield
C. Bakersfield ? Fresno ? Los Angeles ? San Diego ? Las Vegas ? Bakersfield
D. Bakersfield ? Fresno ? Las Vegas ? Los Angeles ? San Diego ? Bakersfield
Answer: C
You might also like to view...
Perform the indicated operation.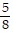
? 
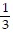
A.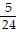 
B. 
C.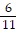 
D.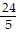 
Solve.A polygon with n sides has D diagonals, where D is given by the function D(n) = 
. Find the number of sides n if 54 ? D ? 135.
A. {n|12 ? n ? 18} B. {n|11 ? n ? 19} C. {n|13 ? n ? 18} D. {n|10 ? n ? 19}
Find the expected value.Mr. Cameron is sponsoring an summer concert. He estimates that he will make $300,000 if it does not rain and make $60,000 if it does rain. The weather bureau predicts the chance of rain is 0.34 for the day of the concert. An insurance company is willing to insure the concert for $150,000 against rain for a premium of $30,000. If he buys this policy, what are his expected earnings from the concert?
A. $180,000 B. $300,000 C. $270,000 D. $239,400
Solve the problem.The line graph represents the gallons of water in a swimming pool after x hours. There is a pump that can either add or remove water from the pool. Find the slope of each line segment, and interpret each slope as a rate of change. Describe what happens to the amount of water in the pool.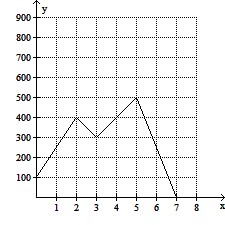
A. Initially the pool contains 100 gallons of water. The pump adds water at a rate of 300 gallons per hour for one hour until there are 400 gallons of water in the pool. For the next hour the pump removes water at a rate of 50 gallons per hour. Then the pump adds water at a rate of 150 gallons per hour for two hours. Finally, the pump removes water at a rate of 150 gallons per hour for 2 hours, at which time the pool is empty. B. Initially the pool contains 1000 gallons of water. The pump removes water at a rate of 150 gallons per hour for two hours until there are 400 gallons of water in the pool. For the next hour the pump adds water at a rate of 100 gallons per hour. Then the pump removes water at a rate of 100 gallons per hour for two hours. Finally, the pump adds water at a rate of 250 gallons per hour for 2 hours, at which time the pool contains 900 gallons of water. C. Initially the pool contains 100 gallons of water. The pump adds water at a rate of 150 gallons per hour for two hours until there are 400 gallons of water in the pool. For the next hour the pump removes water at a rate of 100 gallons per hour. Then the pump adds water at a rate of 100 gallons per hour for two hours. Finally, the pump removes water at a rate of 250 gallons per hour for 2 hours, at which time the pool is empty. D. Initially the pool contains 200 gallons of water. The pump adds water at a rate of 150 gallons per hour for two hours until there are 400 gallons of water in the pool. For the next hour the pump neither adds nor removes water. Then the pump adds water at a rate of 100 gallons per hour for one hour. Finally, the pump removes water at a rate of 250 gallons per hour for 3 hours, at which time the pool is empty.