Complete the following:(a) Use the Leading Coefficient Test to determine the graph's end behavior.(b) Find the x-intercepts. State whether the graph crosses the x-axis or touches the x-axis and turns around at each intercept.(c) Find the y-intercept.(d) Graph the function.f(x) = (x + 2)(x - 3)2
What will be an ideal response?
(a) falls to the left and rises to the right
(b) x-intercepts: (3, 0), touches x-axis and turns; (-2, 0), crosses x-axis
(c) y-intercept: (0, 18)
(d) 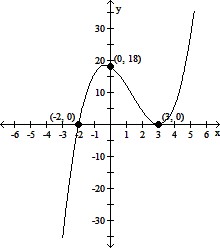
You might also like to view...
Find the exact function value.csc-1(-2)
A. - 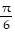
B. 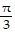
C. 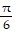
D. - 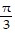
Solve the problem.A company that produces appliances has found that revenue from the sales of the appliances is $50 per appliance, less sales costs of $250. Production costs are $400, plus $40 per appliance. Profit (P) is given by revenue (R) less cost (C), so the company must find the production level x that makes P > 0, that is, R - C > 0.(a) Write an expression for revenue, R, letting x represent the production level (number of appliances to be produced.)(b) Write an expression for production costs C in terms of x.(c) Write an expression for profit P, and then solve the inequality P > 0.(d) Describe the solution in terms of the problem.
A. (a) R = 50x - 250;
(b) C = 400 + 40x;
(c) P = (50x - 250) - (400 + 40x) = 5x - 650; 5x > 650; x > 130
(d) To make a profit, more than 130 appliances must be produced and sold.
B. (a) R = 50x + 250;
(b) C = 400 - 40x;
(c) P = (50x + 250) - (400 - 40x) = 10x - 150; 10x > 150; x > 15
(d) To make a profit, more than 15 appliances must be produced and sold.
C. (a) R = 50x - 250;
(b) C = 400 +
Determine whether the given value is a solution of the inequality.7x + 8 > 29, x = 5
A. No B. Yes
Provide the proper response.Areas of complicated regions are estimated by filling in with shapes whose area is easy to compute. The shape that is most often used in defining the definite integral is ? .
A. the square B. the circle C. the triangle D. the rectangle