There are three genes in the gene pool for blood, A, B, and O. Two of these three are present in a person's blood: A and B dominate O, whereas A and B are codominant. This gives the following possibilities:
Genotype
Phenotype
AAtype A bloodAOtype A bloodABtype AB bloodBOtype B bloodBBtype B bloodOOtype O bloodLet p, q, and r represent the frequencies of the genes A, B, and O in the blood gene pool. Suppose a certain population has 40% type A, 37% type B, and 23% type O. Construct a Punnett square and find (p + q + r) 2 to answer, what percent of the population has each genotype.
A. AA = 16%, AO = 18.4%, AB = 29.6%, BO = 19.02%, BB = 12.69%, OO = 4.29%
B. AA = 16%, AO = 19.4%, AB = 30.6%, BO = 15.02%, BB = 13.69%, OO = 3.29%
C. AA = 18%, AO = 19.4%, AB = 30.6%, BO = 16.02%, BB = 12.69%, OO = 3.29%
D. AA = 17%, AO = 20.4%, AB = 30.6%, BO = 16.02%, BB = 12.69%, OO = 3.29%
E. AA = 16%, AO = 18.4%, AB = 29.6%, BO = 17.02%, BB = 13.69%, OO = 5.29%
Answer: E
You might also like to view...
Solve the problem by writing an appropriate system of equations and using the inverse of the coefficient matrix to solve the system.A grain dealer sold to one customer 5 bushels of wheat, 2 of corn, and 3 of rye, for $39.60; to another, 2 of wheat, 3 of corn, and 5 of rye, for $34.80; and to a third, 3 of wheat, 5 of corn, and 2 of rye, for $33.60. Which of the grains was the cheapest?
A. Wheat B. Wheat and rye (tie) C. Corn and rye (tie) D. Corn
Perform the indicated operation.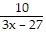
+ 
A. 
B. 
C.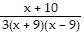 
D. 
Solve the problem.A shop keeper is making a triangular sign for his store front, but he must keep the sign under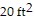 
to adhere to zoning laws. If the base of the sign is 10 ft, what is the maximum height of the triangular sign?
A. 2 ft B. 1 ft C. 30 ft D. 4 ft
Find the indicated function.The weekly revenue and cost functions for a manufacturer of toys are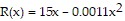 
and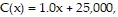 
where x denotes the number of toys produced. What is the weekly profit function? Note: Profit = Revenue - Cost.
A. P(x) = -0.0011x2 + 14x + 25,000 B. P(x) = -0.0011x2 + 16x - 25,000 C. P(x) = -0.0011x2 + 14x - 25,000 D. P(x) = -0.0011x2 + 16x + 25,000