Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n. n = 35n
n = 35n
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 35 = 3(5?1) = 35
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
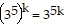 is true for some positive integer k.
is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
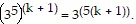
So we assume that 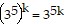 is true and multiply the next term,
is true and multiply the next term, 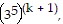 to both sides of the equation.
to both sides of the equation.
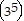 k
k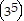 (k + 1) = 35k
(k + 1) = 35k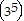 (k + 1)
(k + 1)
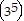 (k + (k + 1)) = 35k
(k + (k + 1)) = 35k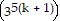
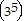 (2k + 1) = 3(5k + 5k + 5))
(2k + 1) = 3(5k + 5k + 5))
3(5(2k + 1)) = 3(5(2k + 1))
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Perform the subtraction. 
A. 352 B. 344 C. 1,040 D. 252
Write fraction notation for the given decimal notation. Do not simplify.-0.174
A. - 
B. - 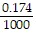
C. - 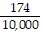
D. - 
Solve the rational inequality. Express the solution in interval notation.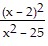 > 0
> 0
A. (-5, 2) ? (5, ?) B. (-?, -5) ? (5, ?) C. (-5, 2) ? (2, 5) D. (-?, -5) ? (2, 5)
Find the dot product v ? w.v = -4i, w = -3j
w = -3j
A. 0 B. 12 C. -7 D. 5