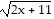Solve the problem.A furniture company makes two different types of lamp stand. Each lamp stand A requires 20 minutes for sanding, 48 minutes for assembly, and 6 minutes for packaging. Each lamp stand B requires 9 minutes for sanding, 32 minutes for assembly, and 8 minutes for packaging. The total number of minutes available each day in each department are as follows: for sanding 3600 minutes, for assembly 9600 minutes, and for packaging 2000 minutes. The profit on each lamp stand A is $30 and the profit on each lamp stand B is $22. How many of each type of lamp stand should the company make per day to maximize their profit? What is the maximum profit?
A. Maximum profit is $6850 when they make 100 of lamp stand A and 175 of lamp stand B.
B. Maximum profit is $5400 when they make 180 of lamp stand A and 0 of lamp stand B.
C. Maximum profit is $6380 when they make 66 of lamp stand A and 200 of lamp stand B.
D. Maximum profit is $6164 when they make 138 of lamp stand A and 92 of lamp stand B.
Answer: C
You might also like to view...
Provide an appropriate response.Consider these two problems:(A) Solve this equation (x + 5)2 = 225. (B) Solve this equation (x + 5)2 = - 225.What is the answer to part (A) and (B) , and why are the answers to each part different?
What will be an ideal response?
Evaluate the function.Find f(12) f
A. (7, 4) B. None of these C. 7 D. 4
Simplify each side of the equation, if possible. Then solve the equation.-2a + 5 + 3a = 10 - 20
A. -15 B. 15 C. 35 D. -35
Evaluate the function as indicated.Find g(x + 4) when g(x) = 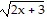 .
.
A. 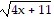
B. 
C. 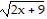
D.