Sketch the graph of the equation. Identify the vertex and the intercepts.y = - x2 - 2x - 1
A. Vertex: (-1, 0);
x-intercept: (-1, 0);
y-intercept: (0, 1)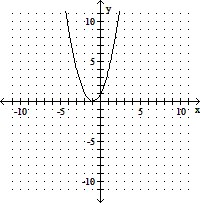
B. Vertex: (1, 0);
x-intercept: (1, 0);
y-intercept: (0, 1)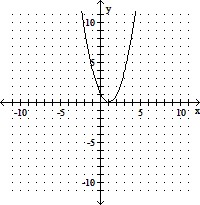
C. Vertex: (-1, 0);
x-intercept: (-1, 0);
y-intercept: (0, -1)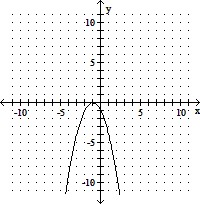
D. Vertex: (1, 0);
x-intercept: (1, 0);
y-intercept: (0, -1)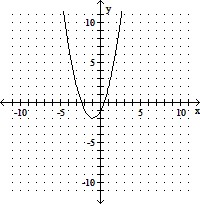
Answer: C
You might also like to view...
Suppose u and v are differentiable functions of x. Use the given values of the functions and their derivatives to find the value of the indicated derivative.u(1) = 4, u '(1) = -7, v(1) = 6, v '(1) = -4.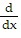
(2u - 4v) at x = 1
A. -16 B. -30 C. 32 D. 2
Use the vertex and intercepts to sketch the graph of the equation. Give the equation for the parabola's axis of symmetry.x = - 2y2 + 12y - 14
A. Axis of symmetry is x = 3.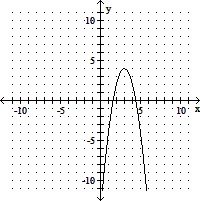
B. Axis of symmetry is y = -3.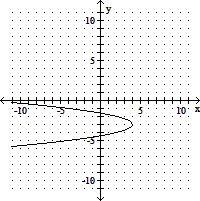
C. Axis of symmetry is x = -3.
D. Axis of symmetry is y = 3.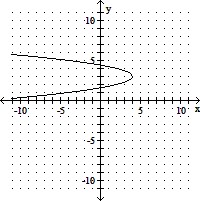
A tangent to a circle and a radius of that circle to the point of tangency are ___________________.
What will be an ideal response?
Use a graphing utility to find the equation of the line of best fit. Round to two decimal places, if necessary.
A. y = 0.43x + 1.79 B. y = -1.86x + 1.79 C. y = 1.79x - 1.86 D. y = 1.79x + 0.43