Provide an appropriate response.(a) Graph the curves r =  and r =
and r = 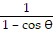 .(b) Find polar coordinates of the points of intersection of the curves in part (a).(c) Show that at the points of intersection the tangent lines to the curves are perpendicular to each other.
.(b) Find polar coordinates of the points of intersection of the curves in part (a).(c) Show that at the points of intersection the tangent lines to the curves are perpendicular to each other.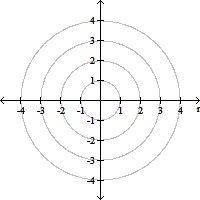
What will be an ideal response?
(a)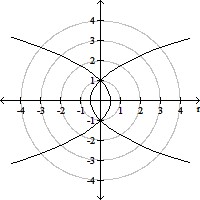
(b) The curves intersect in two points. In polar coordinates, these points may be represented by 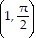 and
and 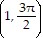 .
.
(c) For r = 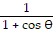 ,
,  = -cot
= -cot 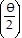 . For r =
. For r = 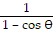 ,
, 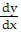 = tan
= tan 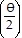 . Thus the slopes of the tangent lines to the curves at both of the points of intersection are negative reciprocals of each other so the tangent lines are perpendicular.
. Thus the slopes of the tangent lines to the curves at both of the points of intersection are negative reciprocals of each other so the tangent lines are perpendicular.
You might also like to view...
Two points on L1 and two points on L2 are given. Determine whether L1 is parallel to L2, L1 is perpendicular to L2, or neither.L1: (3, -3), (8, -5); L2: (1, -3), (11, -7)
A. parallel B. perpendicular C. neither
Find the value of r and determine if a correlation exists at the indicated level of significance. ?? = 0.01
?? = 0.01
A. r = 0.9418; Correlation does not exist. B. r = 0.9657; Correlation exists. C. r = 0.9646; Correlation exists. D. r = 0.9353; Correlation does not exist.
Divide. Write the answer in lowest terms and as a whole or mixed number where possible.
A. 2
B. 6
C. 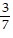
D. 3
Evaluate the integral by using a substitution prior to integration by parts.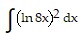
A. x 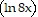 2 - 2x
2 - 2x 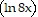 + C
+ C
B. x 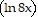 2 - x
2 - x 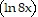 + x + C
+ x + C
C. x 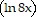 2 + 2x
2 + 2x 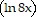 - 2x + C
- 2x + C
D. x 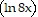 2 - 2x
2 - 2x 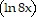 + 2x + C
+ 2x + C