Determine whether the two matrices are inverses of each other by computing their product.
and 
A. No
B. Yes
Answer: B
You might also like to view...
Use the distributive property to rewrite the expression.5(5r + 6 + 2s)
A. 25r + 30 + 10s B. 25r + 30 + 2s C. 25r + 6 + 2s D. 25r + 6 + 10s
Solve the problem.A space heater can raise the temperature in a room by 2°F every 5 minutes. The temperature in the room was 69°F after the heater had been running for 10 minutes. (i) Write as a linear equation in slope-intercept form the relationship between the time that the heater has been running and the temperature in the room.(ii) Explain how you could have predicted whether the slope of the graph of this equation is positive or negative.
A. (i) y =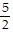 
x - 65
(ii) As the amount of time the space heater is left on increases, the temperature of the room increases, which implies a positive slope.
B. (i) y =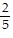 
x + 65
(ii) As the amount of time the space heater is left on increases, the temperature of the room increases, which implies a positive slope.
C. (i) y =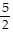 
x + 65
(ii) As the amount of time the space heater is left on increases, the temperature of the room increases, which implies a positive slope.
D. (i) y =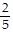 
x - 65
(ii) As the amount of time the space heater is left on increases, the temperature of the room increases, which implies a positive slope.
Determine whether the expression is a monomial. If it is a monomial, state the coefficient and degree.-6x7
A. monomial; coefficient -6; degree 7 B. monomial; coefficient 7; degree 0 C. not a monomial D. monomial; coefficient 7; degree -6
Write the sample space for the experiment. A box contains 3 blue cards numbered 1 through 3, and 4 green cards numbered 1 through 4. Bill picks a blue card and then a green card and records the number on each card.
A. S = {(1, 2, 3, 4)} B. S = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (4, 3)} C. S = {(3, 4)} D. S = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4)}