Find the vertex, focus, and directrix of the parabola with the given equation.(y + 3)2 = -4(x - 4)
A. vertex: (4, -3)
focus: (5, -3)
directrix: x = 3
B. vertex: (-3, 4)
focus: (-4, 4)
directrix: x = -2
C. vertex: (-4, 3)
focus: (-5, 3)
directrix: x = -3
D. vertex: (4, -3)
focus: (3, -3)
directrix: x = 5
Answer: D
You might also like to view...
Find the standard-form equation of the hyperbola centered at the origin which satisfies the given conditions.Foci at (-5, 0), (5, 0); asymptotes: y =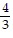 
x, y = - 
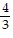x
A. 
- 
= 1
B. 
- 
= 1
C. 
- 
= 1
D. 
- 
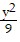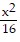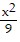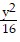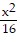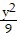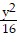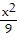= 1
Solve the problem.Find the area of the shaded region.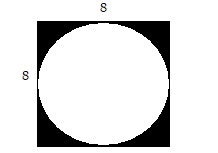
A. 64 - 16? units2 B. 64 - 32? units2 C. 256 - 64? units2 D. 16? + 64 units2
Write an equation in slope-intercept form of a line satisfying the given conditions.m =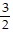 
; b = -4
A. y = -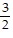 
x + 4
B. y = - 
x - 4
C. y = 
x + 4
D. y = 
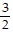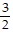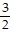x - 4
Solve for the specified variable.A =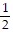 
bh for b
A. b = 
B. b =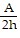 
C. b =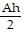 
D. b = 