Use Identities to find the exact value.cos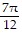 
cos 
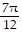+ sin 
sin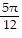 
A.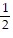 
B.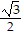 
C.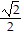 
D. - 1
Answer: B
You might also like to view...
Divide using synthetic division.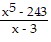
A. x4 + 3x3 + 9x2 + 27x + 81 +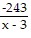 
B. x4 + 3x3 + 3x2 + 3x + 3
C. x4 + 3x3 + 9x2 + 27x + 81
D. x4 - 3x3 + 9x2 - 27x + 81
Solve the problem.If two resistors are connected in parallel, the total impedance is given by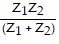 
. Find the total impedance ZT when the impedances Z1 = -8 + 1j and Z2 = 8 - 3j are in parallel. 
?Parallel Circuit
A. - 
B. 
C. = - 8 + 
j
D. - 16 - 
j
Write an equation for the line described. Give your answer in slope-intercept form.slope 0, y-intercept 
A. y = -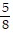 
x
B. y = -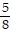 
C. x = - 
D. y = 
x
Solve the problem.The gas mileage, m, of a compact car is a linear function of the speed, s, at which the car is driven, for 
For example, from the graph we see that the gas mileage for the compact car is 45 miles per gallon if the car is driven at a speed of 
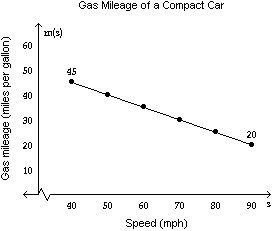Find and interpret the average rate of change in gas mileage between speeds of 40 mph and 90 mph.
A. -0.5 miles per gallon/mph; Between speeds of 40 mph and 90 mph, gas mileage decreases at a rate of 0.5 miles per gallon for each 1 mph increase in speed. B. -0.75 miles per gallon/mph; Between speeds of 40 mph and 90 mph, gas mileage decreases at a rate of 0.75 miles per gallon for each 1 mph increase in speed. C. 0.5 miles per gallon/mph; Between speeds of 40 and 90 mph, gas mileage increases at a rate of 0.5 miles per gallon for each 1 mph increase in speed. D. -0.5 miles per gallon/mph; Between speeds of 40 and 90 mph, speed decreases at a rate of 0.5 miles per hour for each 1 mpg increase in gas mileage.