Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.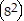
n = 82n
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 82 = 8(2?1) = 82
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
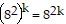is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
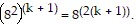
So we assume that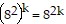 
is true and multiply the next term, 
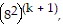to both sides of the equation.
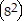k
(k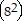 + 1) = 82k
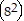(k + 1)
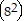(k + (k + 1)) = 82k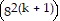
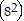(2k + 1) = 8(2k + 2k + 2))
8(2(2k + 1)) = 8(2(2k + 1))
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
It costs $624 to rent a dining hall for a dinner you are catering. In addition it costs $33 for each person attending the dinner.
?
A: Write a formula for the total cost C, in dollars, of catering a dinner for n guests.
?
B: Explain in practical terms the meaning of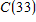 
.
?
C. Calculate the value you found in part B.
What will be an ideal response?
The function f is one-to-one. Find its inverse.f(x) =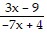 
A. f-1(x) =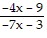 
B. f-1(x) =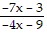 
C. f-1(x) =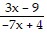 
D. f-1(x) =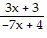 
Solve the problem.Participants in a memorization experiment were able to recall an average of D digits in t minutes, where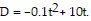 
Use the graph below to find the approximate value of 
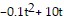for t = 2.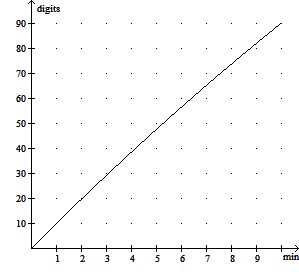
A. 19 digits B. 39 digits C. -1 digits D. 59 digits
Name the conic.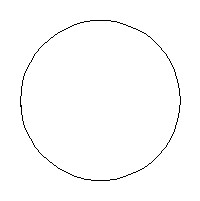
A. parabola B. hyperbola C. circle D. ellipse