Carbon dating presumes that, as long as a plant or animal is alive, the proportion of its carbon that is 14C is constant. The amount of 14C in an object made from harvested plants, like paper, will decline exponentially according to the equation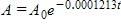 
, where A represents the amount of 14C in the object, Ao represents the amount of 14C in living organisms, and t is the time in years since the plant was harvested. If an archeological artifact has 30% as much 14C as a living organism, how old would you predict it to be? Round to the nearest year.
A. 28,040 years
B. 5715 years
C. 9926 years
D. 14,758 years
E. 100 years
Answer: C
You might also like to view...
Provide an appropriate response.True or False? When the population is small relative to the carrying capacity, logistic growth is exponential with a fractional growth rate close to the base growth rate r.
A. False B. True
Simplify the rational expression.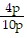
A. 
B.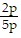 
C. 
D.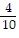 
Solve the problem.The table shows the number of dollars spent in Country X (in millions) on environmental protection programs during the years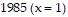 
through 
. Use least-squares regression to find the polynomial function that best models these data. Round coefficients to three decimal places.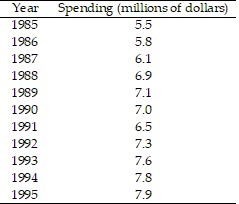 
A. f(x) ? 0.005x3 - 0.102x2 + 0.805x + 4.697 B. f(x) ? -0.010x2 + 0.446x + 5.759 C. f(x) ? 0.007x3 - 0.105x2 + 0.805x + 4.397 D. f(x) ? -0.010x2 + 0.346x + 5.253
Simplify.-5x - 4(x + 4y)
A. -9x - 16y B. -6x - 16y C. -9x + 16y D. -9x + 4y