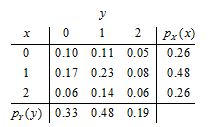
Refer to Exercise 1.
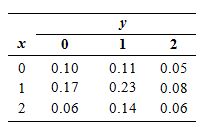
a. Find the marginal probability mass function pX(x).
b. Find the marginal probability mass function pY(y).
c. Find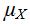 
.
d. Find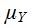 
.
e. Find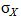 
.
f. Find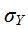
.
g. Find Cov(X, Y).
h. Find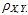
.
i. Are X and Yindependent? Explain.
(a) The marginal probability mass function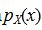 
is found by summing along the rows of the joint probability mass function.
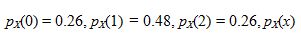= 0 if x?0, 1, or 2
(b)The marginal probability mass function pY(y) is found by summing down the columns of the joint probability mass function. So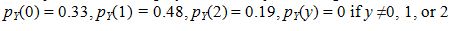 
(c)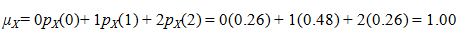 
(d) 
(e)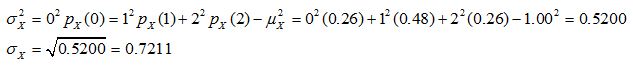 
(f)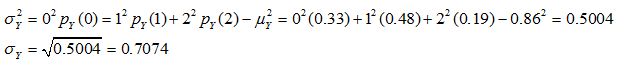 
(g) 
(h) 
(i) No. The joint probability density function is not equal to the product of the marginals. For example, P(X = 0 and Y = 0) = 0.10, but P(X = 0)P(Y = 0) = (0.26)(0.33) = 0.0858.
You might also like to view...
What are four direct benefits of treating cuttings with auxin?
What will be an ideal response?
Caution: ____________________ all circuits before making connections.
Fill in the blank(s) with the appropriate word(s).
To determine an animal's use in breeding, a producer should do which of the following?
A. Transfuse blood B. Analyze ancestry C. Transfer RNA D. No answers
The Toyota engine is based on the ____ cycle.
A. Atkinson B. Foreman C. Atkins D. Joule