Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola.(x + 4)2 - 9(y + 3)2 = 9
A. center at (-3, -4)
transverse axis is parallel to x-axis
vertices at (-6, -4) and (0, -4)
foci at (-3 - 
, -4) and (-3 + 
, -4)
asymptotes of y + 4 = - 
(x + 3) and y + 4 = 
(x + 3)
B. center at (-4, -3)
transverse axis is parallel to x-axis
vertices at (-7, -3) and (-1, -3)
foci at (-4 - 
, -3) and (-4 + 
, -3)
asymptotes of y + 3 = - 
(x + 4) and y + 3 = 
(x + 4)
C. center at (-4, -3)
transverse axis is parallel to y-axis
vertices at (-4, -6) and (-4, 0),
foci at (-4, -3 - 
) and (-4, -3 + 
),
asymptotes of y - 3 = - 3(x - 4) and y - 3 = 3(x - 4)
D. center at (-4, -3)
transverse axis is parallel to x-axis
vertices at (-5, -3) and (-3, -3)
foci at (-4 - 
, -3) and (-4 + 
, -3)
asymptotes of y + 3 = - 3(x + 4) and y + 3 = 3(x + 4)
Answer: B
You might also like to view...
Set up an integral for the area of the surface generated by revolving the given curve about the indicated axis.x =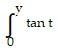 
dt, 0 ? y ? ?/3; y-axis
A. ?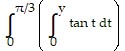
sec y dy
B. ?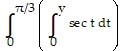
tan y dy
C. 2?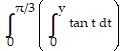
sec y dy
D. 2?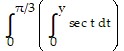
tan y dy
Two formulas that approximate the dosage of a drug prescribed for children are: Young's Rule: C =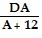 
and Cowling's Rule: C = 
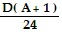.In each formula, A = the child's age in years, D = an adult dosage, and C = the proper child's dosage. The formulas apply for ages 2 through 13. Use these formulas to solve the problem.Use Cowling's Rule to find the difference in a child's dosage for a 10-year-old child and a 6-year old child. Express the answer as a single rational (or fractional) expression in terms of D.
A.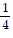 
D
B. 
D
C. 
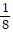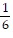D
D. 4D
Graph the values of x that satisfy the given conditions.0 ? x ? 4
A. 
B. 
C. 
D. 
Establish the identity.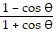
= 
What will be an ideal response?