Solve the problem.A satellite dish is in the shape of a parabolic surface. Signals coming from a satellite strike the surface of the dish and are reflected to the focus, where the receiver is located. The satellite dish shown has a diameter of 10 feet and a depth of 4 feet. The parabola is positioned in a rectangular coordinate system with its vertex at the origin. The receiver should be placed at the focus  The value of p is given by the equation
The value of p is given by the equation 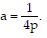 How far from the base of the dish should the receiver be placed?
How far from the base of the dish should the receiver be placed?
src="https://sciemce.com/media/4/ppg__tttt0525191133__f1q96g3.jpg" alt="" style="vertical-align: -4.0px;" />
A. 6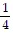 feet from the base
feet from the base
B. 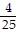 feet from the base
feet from the base
C. 1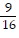 feet from the base
feet from the base
D. 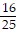 feet from the base
feet from the base
Answer: C
Mathematics
src="https://sciemce.com/media/4/ppg__tttt0525191133__f1q96g3.jpg" alt="" style="vertical-align: -4.0px;" />
A. 6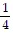 feet from the base
feet from the base
B. 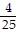 feet from the base
feet from the base
C. 1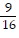 feet from the base
feet from the base
D. 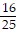 feet from the base
feet from the base
Answer: C
You might also like to view...
Solve using Cramer's rule. 3x - 5y - 2z = -15-2x + 6y - 2z = 20-4x - 4y + 8z = -28
A. (5, 3, 1) B. (4, -5, -1) C. (4, 5, 1) D. (5, 1, 5)
Obtain a slope field and add to its graphs of the solution curves passing through the given points.y' =  with (0, -1)
with (0, -1)
What will be an ideal response?
Solve the problem.One television has a rectangular screen that is 9 inches by 17 inches. Another has a rectangular screen that is 6 inches by 10 inches. The size of a television set is commonly given by the length of the screen's diagonal. What is the difference of the diagonal lengths for these two sets?
A. 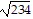 in.
in.
B. (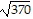 - 2
- 2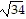 ) in.
) in.
C. 234 in.
D. (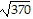 + 2
+ 2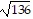 ) in.
) in.
Provide an appropriate response.If 
 = 2, find
= 2, find 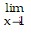 f(x).
f(x).
A. 3 B. 2 C. 1 D. Does not exist