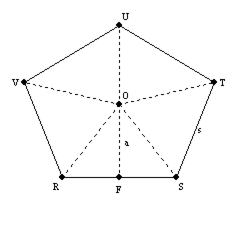
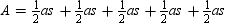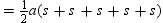Use the drawing provided to explain the following theorem.“The area A of a regular polygon whose apothem has length a and whose perimeteris P is given by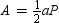 
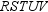
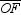
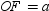
.”Given: Regular polygon 
with center O and length s for each side;apothem 
so that 
Prove:
What will be an ideal response?
, 
, 
, 
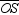, and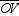 
. Because the radii are congruent to each other and the sides of the regular polygon are all congruent to each other as well, 
, 
, 
, 
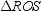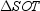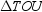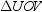, and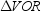 
are all congruent to each other by SSS.Each of the congruent triangles has an altitude length of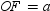 
. Further, the length of each
base of a triangle is s, the length of side of the polygon. Therefore, the area of the regular polygon is
Because the sum of the sides equals perimeter P, we have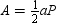 
.
You might also like to view...
Solve the problem.Suppose that the accompanying table shows the velocity of a car every second for 8 seconds. Use the Trapezoidal Rule to approximate the distance traveled by the car in the 8 seconds. Round your answer to the nearest tenth if necessary.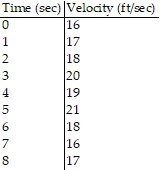
A. 162 ft B. 221.5 ft C. 145.5 ft D. 291 ft
Solve the linear equation using the addition property of equality.6.2p - 10 = 7.2p - 2
A. p = -7 B. p = -8 C. p = -9 D. p = -2
Test the equation for symmetry with respect to the given axis, line, or pole.r2 = sin(2?); the pole
A.
| May or may not be symmetric with respect to the pole |
B. Symmetric with respect to the pole
Express as a difference of logarithms.logg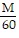 
A. logg M ÷ logg 60 B. logg (M - 60) C. logg 60 - logg M D. logg M - logg 60