Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.6 + 12 + 18 + ... + 6n = 3n(n + 1)
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 6 = 3(1)(1 + 1) = 6.
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
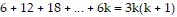is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
So we assume that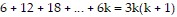 
is true and add the next term, 
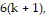to both sides of the equation.
6 + 12 + 18 + ... + 6k + 6(k + 1) = 3k(k + 1) + 6(k + 1)
= (k + 1)(3k + 6)
= 3(k + 1)(k + 2)
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Use a calculator to find the acute angle between the planes to the nearest thousandth of a radian.2x - 8y + 9z = -5 and -6x - 9y + 3z = 4
A. 1.549 rad B. 0.883 rad C. 0.627 rad D. 0.688 rad
Jadwiga determined that the cost of a box of 1000 tongue depressors is $4.85 at TMJ Medical Supply. This cost represents a 2% increase in the price. What was the original price per box before the increase?
A. $4.75 B. $0.10 C. $4.80 D. $4.95
Solve.How many cubic yards of concrete are needed to pour a concrete slab 24 feet long, 14 feet wide and 8 inches thick? Round to the nearest tenth.
Fill in the blank(s) with the appropriate word(s).
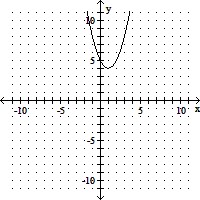
Sketch by hand the graph of the function. Give the coordinates for the vertex.y = x2 - 2x + 5
A. vertex: (1, -4)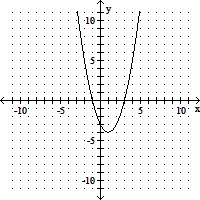
B. vertex: (-1, 4)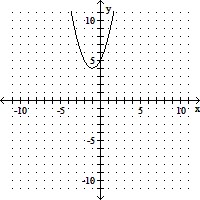
C. vertex: (-1, -4)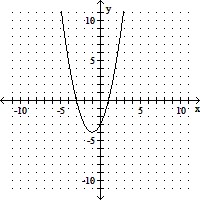
D. vertex: (1, 4)