Solve the problem.The Cobb-Douglas function for a new product is given by 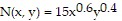 where x is the number of units of labor and y is the number of units of capital required to produce N(x, y) units of the product. Each unit of labor costs $40, and each unit of capital costs $80. If $400,000 has been budgeted for the production of this product, determine how this amount should be allocated in order to maximize production, and find the maximum production.
where x is the number of units of labor and y is the number of units of capital required to produce N(x, y) units of the product. Each unit of labor costs $40, and each unit of capital costs $80. If $400,000 has been budgeted for the production of this product, determine how this amount should be allocated in order to maximize production, and find the maximum production.
A. 2000 units of labor and 6000 units of capital
max N(x,y) = N(2000, 6000) ? 46,555 units
B. 6000 units of labor and 2000 units of capital
max N(x, y) = N(6000, 2000) ? 57,995 units
C. 6000 units of labor and 6000 units of capital
max N(x,y) = N(6000, 6000) ? 89,995 units
D. 2000 units of labor and 2000 units of capital
max N(x,y) = N(2000, 2000) ? 30,195 units
Answer: B
You might also like to view...
Solve the problem.Find the equation of the line through (1, 0) and perpendicular to y = 5x + 3.
A. y = - 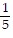 x +
x + 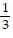
B. y = - 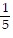 x +
x + 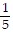
C. y = 5x - 3
D. y = 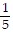 x -
x - 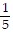
Multiply the polynomials.(5y - 9)(-9y2 - y + 6)
A. -45y3 + 39y - 54 B. -45y3 + 76y2 + 39y - 54 C. -45y3 + 86y2 + 39y - 54 D. -14y2 + 39y - 54
Solve. Provide answers in interval notation.(c + 8)(c - 1)(c - 5) > 0
A. (5, ?) B. (-?, -8) ? (1, 5) C. (-8, 1) ? (5, ?) D. (-?, 1)
Solve the equation.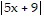 =
= 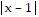
A. {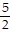 ,
, 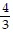 }
}
B. 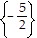
C. {- 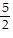 , -
, - 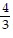 }
}
D. ?