Sketch the graph of the function. Indicate where it is increasing and where it is decreasing. Indicate where any relative extrema occur, where asymptotes occur, where the graph is concave up and where is it concave down, where any points of inflection occur, and where any intercepts occur. f(x) =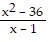 
What will be an ideal response?
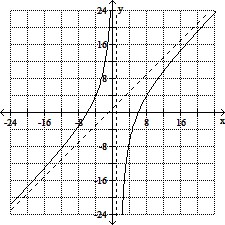
Increasing on (-?, 1), and (1, ?)
No relative extrema
Asymptotes: x = 1 and y = x + 1
Concave up on (-?, 1); concave down on (1, ?)
No points of inflection
y-intercept: (0, 36 ), x-intercepts: (-6, 0) and (6, 0)
You might also like to view...
Solve the problem.A patient takes 100 mg of medication every 24 hours. 80% of the medication in the blood is eliminated every 24 hours.a. Let dn equal the amount of medication (in mg) in the blood stream after n doses, where d1 = 100. Find a recurrence relation for dn.b. Show that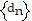 
is monotonic and bounded, and therefore converges.c. Find the limit of the sequence. What is the physical meaning of this limit?
A. a. dn + 1 = 0.2dn + 100, d1 = 100 b. dn satisfies 0 ? dn ? 150 for n ? 1 and its terms are increasing in size. c. 150; in the long run there will be approximately 150 mg of medication in the blood. B. a. dn + 1 = 0.2dn + 100, d1 = 100 b. dn satisfies 0 ? dn ? 125 for n ? 1 and its terms are increasing in size. c. 125; in the long run there will be approximately 125 mg of medication in the blood. C. a. dn + 1 = 0.8dn + 100, d1 = 100 b. dn satisfies 0 ? dn ? 150 for n ? 1 and its terms are increasing in size. c. 150; in the long run there will be approximately 150 mg of medication in the blood. D. a. dn + 1 = 0.8dn + 100, d1 = 100 b. dn satisfies 0 ? dn ? 125 for n ? 1 and its terms are increasing in size. c. 125; in the long run there will be approximately 125 mg of medication in the blood.
Find at least three nonzero terms [including a0, at least two cosine terms (if they are not all zero) and at least two sine terms (if they are not all zero)] of the Fourier series for the given function.f(x) =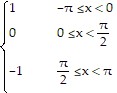 
A. f(x) =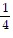 
+ 
- 
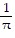
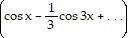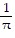(3 sin x - sin 2x + . . .)
B. f(x) =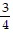 
+ 
- 
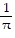
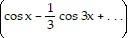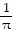(5 sin x - sin 2x + . . .)
C. f(x) =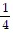 
- 
+ 
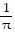
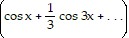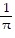
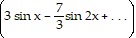
D. f(x) =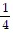 
+ 
- 
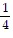
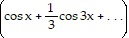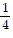(3 sin x - sin 2x + . . .)
Solve the problem.Based on the 2000 U. S. Census, Florida had a standard quota of 24.776. What percent of the U.S. population lived in Florida in 2000? (Use the fact that the House of Representatives has 435 seats.)
A. 5.2% B. 5.7% C. 5.4% D. 10.8% E. 17.6%
Solve the system of equations using matrices.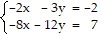
A. (4, 4)
B. (-2, 7)
C. {(x,y)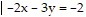 
}
D. ?