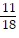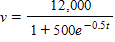You manage a small antique store that owns a collection of Louis XVI jewelry boxes. Their value v is increasing according to the formula
?
?
where t is the number of years from now. You anticipate an inflation rate of 1% per year, so that the present value of an item that will be worth $v in t years' time is given by
?
?
In how many years from now will the greatest rate of increase of the present value of your antiques be attained? Round your answer to two decimal places.
?
A. t = 24.55 years
B. t = 3.07 years
C. t = 11.27 years
D. t = 12.27 years
E. t = 6.14 years
Answer: D
You might also like to view...
Find an equation of the circle with the given center and radius.Center at (-3, 2); radius = 9
A. (x + 3)2 + (y - 2)2 = 81 B. (x - 2)2 + (y + 3)2 = 9 C. (x - 3)2 + (y + 2)2 = 81 D. (x + 2)2 + (y - 3)2 = 9
In a right triangle, find the length of the side not given. Let c represent the length of the hypotenuse. Give an answer to the nearest tenth if necessary.b = 20 cm, c = 25 cm
A. a = 5 cm B. a = 45 cm C. a = 15 cm D. a = 225 cm
Solve the problem.Irene wants to invest $36,000 in stocks, bonds, and gold coins. She knows that her rate of return will depend on the economic climate of the country, which is difficult to predict. After some research and analysis, she determines the annual profit in dollars that she would expect per hundred dollars on each type of investment, depending on whether the economy is strong, stable, or weak.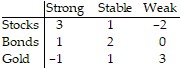 
How should Irene invest her money in order to maximize her profit regardless of what the economy does? In other words, consider the problem as a matrix game in which Irene is playing against "fate".
A. Irene should invest $14,000 in stocks, $8000 in bonds, and $18,000 in gold. B. Irene should invest $12,000 in stocks, $8000 in bonds, and $16,000 in gold. C. Irene should invest $16,000 in stocks and $20,000 in gold. D. Irene should invest $15,000 in stocks and $21,000 in gold.
Solve the equation.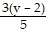
= 1 - 3y
A. y =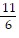 
B. y =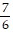 
C. y = -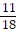 
D. y = 