Rewrite the quadratic equation in the form ax2 + bx + c = 0, then identify a, b, and c. 2x2 + 11 = 0
A. a = 2, b = 0, c = -11
B. a = 0, b = 2, c = 11
C. a = 2, b = 0, c = 11
D. a = 2, b = 11, c = 0
Answer: C
You might also like to view...
Find the extreme values of the function subject to the given constraint.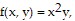
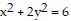
A. Maximum: 4 at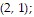 
minimum: -4 at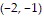 
B. Maximum: 18 at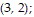 
minimum: -18 at 
C. Maximum: 4 at 
minimum: -4 at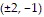 
D. Maximum: 18 at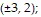 
minimum: -18 at 
Insert parentheses in order to make the statement true. More than one set of parentheses may be needed.4 ? 7 - 2 = 20
A. (4)(7)(-2) = 20 B. 4 ? (7 - 2) = 20 C. 4 ? 7 (-2) = 20 D. (4 ? 7) - 2 = 20
Simplify the expression. Assume that all variables are positive.(x6y9)1/3
A. x18y27 B. x3y2 C. x2y3 D. 3x6y9
Find the function value indicated for the function. If necessary, round to two decimal places. If the function value is not a real number and does not exist, state so.Evaluate m(x) = -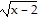
for m(27)
A. 5 B. not a real number C. -5 D. m( -5 )