Solve the problem.Big Round Cheese Company has on hand 45 pounds of Cheddar and 49 pounds of Brie each day. It prepares two Christmas packages-the "Holiday" box, which has 5 pounds of Cheddar and 2 pounds of Brie, and the "Noel" box, which contains 2 pounds of Cheddar and 7 pounds of Brie. Profit on each Holiday assortment is $6, profit on each Noel assortment is $8. Determine the number of boxes of each assortment that will maximize profits for Big Round Cheese Company given the initial and final tableaux:?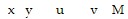
?
src="https://sciemce.com/media/4/ppg__tttt0625191415__f1q61g3.jpg" style="vertical-align: -49.0px;" />(initial)(final)Here, x = the number of Holiday boxes per day and y = the number of Noel boxes per day.One day Big Round gets a total of 80 pounds of Brie. How should the production schedule change to maximize profit? What is the new profit?
What will be an ideal response?
x = 5, y = 10, M = $110
Mathematics
src="https://sciemce.com/media/4/ppg__tttt0625191415__f1q61g3.jpg" style="vertical-align: -49.0px;" />(initial)(final)Here, x = the number of Holiday boxes per day and y = the number of Noel boxes per day.One day Big Round gets a total of 80 pounds of Brie. How should the production schedule change to maximize profit? What is the new profit?
What will be an ideal response?
x = 5, y = 10, M = $110
You might also like to view...
Solve the problem.Consider the area of the region in the first quadrant enclosed by the curve y =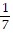 
cosh 7x, the coordinate axes, and the line x = 8. This area is the same as the area of a rectangle of a length s, where s is the length of the curve from 
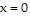to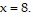 
What is the height of the rectangle?
A.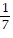 
B.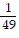 
sinh 56
C. 7
D. sinh 56
Provide an appropriate response. Solve for the variable: 2.5x + 2.4 = -6.7
A. -1.72 B. -3.64 C. 6.6 D. 1.72
Complete the identity.
= ?
A. sec2 x B. 1 C. cot2 x D. csc2 x
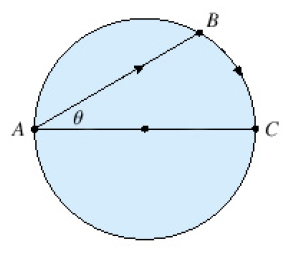
A woman at a point A on the shore of a circular lake with radius 4mi wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of 6mi/h and row a boat at 2mi/h. How should she proceed? (Find ?). Round the result, if necessary, to the nearest hundredth.
