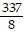Solve the problem.The gas mileage, m, of a compact car is a linear function of the speed, s, at which the car is driven, for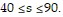 
For example, from the graph we see that the gas mileage for the compact car is 45 miles per gallon if the car is driven at a speed of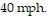 
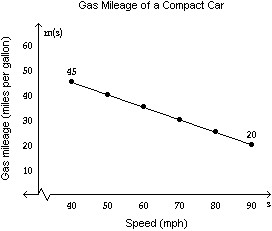i) Using the two points on the graph, determine the function m(s) that can be used to approximate the graph.ii) Using the function from part i, estimate the gas mileage if the
compact car is traveling 81 mph. If necessary, round to the nearest tenth.iii) Using the function from part i, estimate the speed of the compact car if the gas mileage is 36 miles per gallon. If necessary, round to the nearest tenth.
A. i) m(s) = -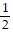 
s + 65
ii) 105.5 miles per gallon
iii) 58 mph
B. i) m(s) = -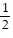 
s + 65
ii) 24.5 miles per gallon
iii) 58 mph
C. i) m(s) = -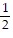 
s + 65
ii) 24.5 miles per gallon
iii) 63 mph
D. i) m(s) =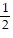 
s + 65
ii) 105.5 miles per gallon
iii) 58 mph
Answer: B
You might also like to view...
Create a graph with the given properties.Two even and four odd vertices
What will be an ideal response?
Graph the region determined by the inequality in the context of the application.A hardware store has room for 300 bags of fertilizer. The fertilizer manufacturer plans to ship x bags of fertilizer with a 
and y bags of fertilizer without the weed killer. This can be represented by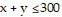 
.
A.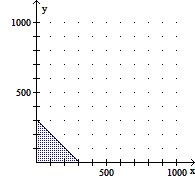 
B. 
C.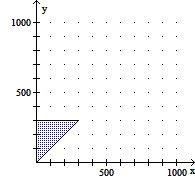 
D.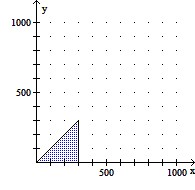 
Simplify the expression.-2(10r + 4) + 10(7r + 2)
A. 8r + 2 B. 50r + 4 C. -28r D. 50r + 12
Use n = 4 to approximate the value of the integral by the trapezoidal rule.
A.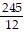 
B.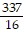 
C.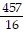 
D. 