Solve the problem.The population P, in thousands, of Jonesburg is given byP(t) =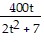 
,
where t is the time, in months.Graph the function on the interval [0,?) and complete the following:P(t) ? 
as t ? ?.
A. 
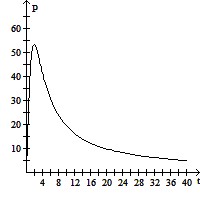
P(t) ? 0 as t ? ?.
B. 
P(t) ? 1 as t ? ?.
C.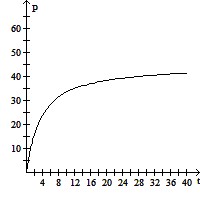 
P(t) ? 50 as t ? ?.
D.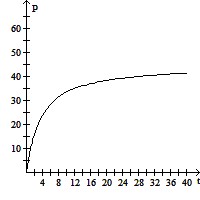 
P(t) ? 45 as t ? ?.
Answer: A
You might also like to view...
Find the equation of the parabola which has the given vertex V, which passes through the given point P, and which has the specified axis of symmetry.V (1, -2), P(21, -4), horizontal axis of symmetry
A. (x - 1)2 =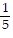 
(y + 2)
B. (x + 1)2 =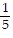 
(y - 2)
C. (y + 2)2 =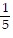 
(x - 1)
D. (y - 1)2 =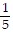 
(x + 2)
Solve the absolute value equation.|4x + 6| = |x + 1|
A. x =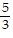 
, 
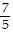
B. x = -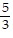 
, 
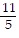
C. x = -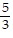 
, - 
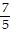
D. no solution
Graph the region that satisfies the constraints.A contractor builds two models of homes, the Raskolnikov and the Karamazov. The Raskolnikov requires 180 worker-days of labor and $300,000 in capital, while the Karamazov requires 270 worker-days of labor and $200,000 in capital. The contractor has a total of 5400 worker-days and $6,000,000 in capital available per month. Let x represent the number of Raskolnikov models and y represent the number of Karmazov models.
A.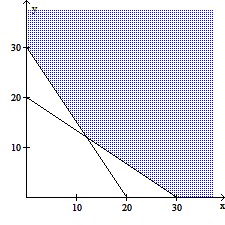 
B.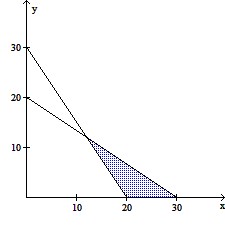 
C.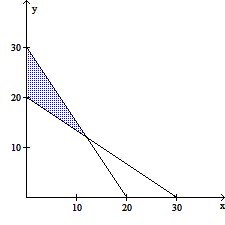 
D.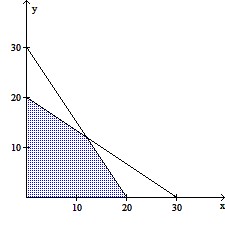 
Solve. Assume the exercise describes a linear relationship. When writing a linear equation, write the equation in slope-intercept form.A faucet is used to add water to a large bottle that already contained some water. After it has been filling for 5 seconds, the gauge on the bottle indicates that it contains 17 ounces of water. After it has been filling for 11 seconds, the gauge indicates the bottle contains 35 ounces of water. Let y be the amount of water in the bottle x seconds after the faucet was turned on. Write a linear equation that models the amount of water in the bottle in terms of x.
A. y =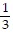 
x +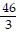 
B. y = 3x + 2
C. y = 3x + 24
D. y = -3x + 32