Graph the equation.y = 
A. 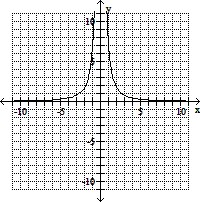
B. 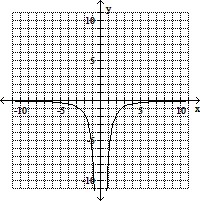
C. 
D. 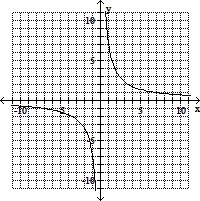
Answer: A
You might also like to view...
Provide an appropriate response.What effect does a 135° rotation of the coordinate axes have on the equation of the hyperbola xy = 1? Give the new equation.
A. -uv = 1
B. u2 - v2 = 1
C. -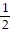 u2 +
u2 + 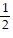 v2 = 1
v2 = 1
D. 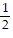 u2 -
u2 - 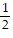 v2 = 1
v2 = 1
Find the requested term in the sequence.The nth term in 15, 30, 45, 60, 75, . . .
A. 15n + 2 B. 15n C. 15n + 15 D. 15n - 15
Provide an appropriate response.Find the volume of the cone. 
A. 34.2 in3 B. 136.7 in3 C. 131.2 in3 D. 32.8 in3
Solve the problem.A company that produces appliances has found that revenue from the sales of the appliances is $50 per appliance, less sales costs of $250. Production costs are $400, plus $40 per appliance. Profit (P) is given by revenue (R) less cost (C), so the company must find the production level x that makes P > 0, that is, R - C > 0.(a) Write an expression for revenue, R, letting x represent the production level (number of appliances to be produced.)(b) Write an expression for production costs C in terms of x.(c) Write an expression for profit P, and then solve the inequality P > 0.(d) Describe the solution in terms of the problem.
A. (a) R = 50x - 250;
(b) C = 400 + 40x;
(c) P = (50x - 250) - (400 + 40x) = 5x - 650; 5x > 650; x > 130
(d) To make a profit, more than 130 appliances must be produced and sold.
B. (a) R = 50x + 250;
(b) C = 400 - 40x;
(c) P = (50x + 250) - (400 - 40x) = 10x - 150; 10x > 150; x > 15
(d) To make a profit, more than 15 appliances must be produced and sold.
C. (a) R = 50x - 250;
(b) C = 400 +