If six integers are chosen from the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, must there be at least two integers with the property that the sum of the smaller plus the larger is 11? Why or why not? Write an answer that would convince a good but skeptical fellow student who has learned the statement of the pigeonhole principle but not seen an application like this one. Either describe the pigeons, the pigeonholes, and how the pigeons get to the pigeonholes, or describe a function by giving its domain, co-domain, and how elements of the domain are related to elements of the co-domain.
What will be an ideal response?

Mathematics
You might also like to view...
Graph the function.g(x) = log1/5 x
A. 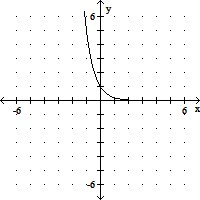
B. 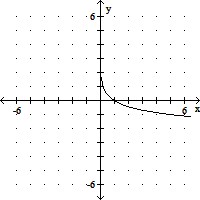
C. 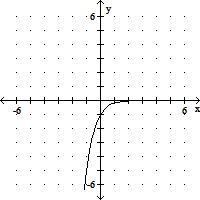
D. 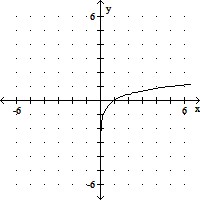
Mathematics
Use a graphing calculator to estimate the local maximum and local minimum values of the function to the nearest hundredth.y = 3x3 - 4x2 - 6x + 2
A. Loc max value 3.17, loc min value 1.60 B. Loc max value 1.60, loc min value -0.71 C. Loc max value 3.63, loc min value -6.01 D. Loc max value -0.71, loc min value -5.56
Mathematics
Solve.3(4x - 1) = 12
A. 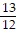
B. 
C. 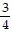
D. 
Mathematics
For the functions f and g, find the requested value.Evaluate (f ? g)(2).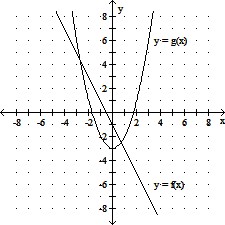
A. -4 B. 0 C. -3 D. -5
Mathematics