Solve the problem.The floor plan of a building is shown in the figure below. Is it possible to start in one of the rooms of the building, walk through each door exactly once, and end up in a different room from the one you started in? (Consider the outside a "room".) Justify your answer.
What will be an ideal response?
No. Each room (including "outside") has an even number of doors. Thus, an Euler path starting and ending in different rooms is not possible.
You might also like to view...
Find the area or volume.Find the area under y =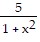 
in the first quadrant.
A. 5?
B. 10?
C. 
?
D.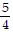 
?
Multiply 4/31è ð 11/72è
What will be an ideal response?
Provide an appropriate response.Give the sign of the three trigonometric functions of the vector with the endpoint (0, 5).
A. sine, positive; cosine, negative; tangent, positive B. sine, positive; cosine, zero; tangent, undefined C. sine, negative; cosine, positive; tangent, positive D. sine, zero; cosine, positive; tangent, zero
Find the domain and range of the inverse of the given function.f(x) = - 
A. Domain: all real numbers; range: (-?, 0) ? (0, ?) B. Domain and range: (-?, 0) ? (0, ?) C. Domain and range: all real numbers D. Domain: (-?, 0) ? (0, ?); range: (-?, 0)