Find the standard-form equation of the ellipse centered at the origin and satisfying the given conditions.An ellipse with vertices (±6, 0) and foci at (±5, 0)
A. 
+ 
= 1
B. 
+ 
= 1
C. 
+ 
= 1
D. 
+ 
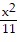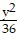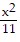= 1
Answer: D
You might also like to view...
Provide an appropriate response.Find the value(s) of t corresponding to the extrema of f(x, y, z) = sin(x2 + y2)cos(z) subject to the constraints x2 + y2 = 3t, 
and z =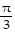 
. Classify each extremum as a minimum or maximum. (Hint: w = f(x, y, z) is a differentiable function of t.)
A. t = -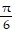 
, maximum
B. t =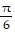 
, minimum; t = - 
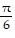, maximum
C. t =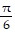 
, minimum; t = 0, maximum
D. t =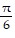 
, minimum
Factor by grouping.3x2 - 9xy + 5xy - 15y2
A. (3x - 5y)(x - 3y) B. (3x + 5y)(x + 3y) C. (3x2 + 5y)(1 - 3y) D. (3x + 5y)(x - 3y)
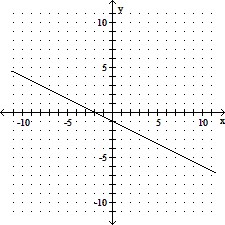
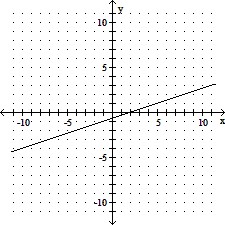
Find the x- and y-intercepts of the graph of the given equation, if they exist. Then graph the equation.9y - 3x = -6
A. x: -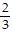 
; y: 2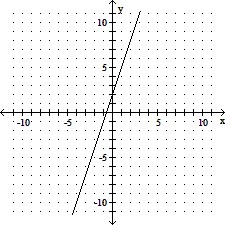 
B. x: -2; y: -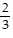 
C. x: 2; y: - 
D. x: -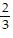 
; y: -2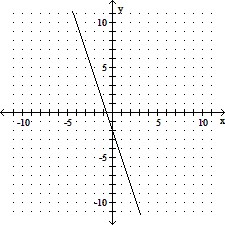 
A small town has only two dry cleaners, Fast and Speedy. Fast hopes to increase its market share by conducting an extensive advertising campaign. The initial market share for Fast was 40% and 60% for Speedy. Solve the problem.Use the initial market share as an initial distribution matrix, along with the following stochastic matrix, to find the market share for each firm for the second batch of clothing after the campaign. Round your answer to the nearest percent.FastSpeedy 
A. 68% for Fast and 33% for Speedy B. 53% for Fast and 47% for Speedy C. 33% for Fast and 68% for Speedy D. 47% for Fast and 53% for Speedy